Giải thưởng Toán Học CLAY

Vietsciences-Trần Điển Ngọc       28/02/2005   Cập nhật   20/08/2010

 

Viện Toán học Clay [Clay Mathematical Institute (CMI)]  là một tổ chức tư nhân được Landon T. Clay, một thương gia người Boston và vợ là Lavinia D. Clay tài trợ và tạo lập tháng 9 năm 1998, tại thành phố Cambridge, tiểu bang Massachusetts, Hoa kỳ.   Mục tiêu Viện đề ra "để khuếch trương và phổ biến các hiểu biết toán học, để hướng dẫn các nhà toán học và các khoa học gia khác về những khám phá mới trong phạm vi toán học, để khuyến khích các sinh viên có biệt tài theo đuổi ngành toán học, và để ghi nhận những thành quả và tiến bộ đặc biệt trong việc nghiên cứu toán học."  

Theo đuổi mục đích này, Viện Toán học Clay bảo trợ công việc nghiên cứu của nhiều khoa học gia, tổ chức những lớp Toán thâm cứu đặc biệt vào mùa hè, và trao hai giải thưởng: Giải thưởng Nghiên cứu hàng năm (Clay Research Award) và Giải Thiên niên kỷ. (Millenium Prize Problems).

 1- Giải thưởng Nghiên cứu hàng năm

            Giải thưởng Nghiên cứu hàng năm (Clay Research Award) được dành cho những công trình khám phá toán học siêu việt đã được thực hiện trong năm trước đó. 

* Năm 1999 Viện đã trao giải cho Andrew Wiles (chứng minh định lý Fermat, đề ra cách đây hơn 358 năm).  Xin giới thiệu đến quý độc giả quyển Định  Lý Cuối Cùng Của FERMAT , tác giả Simon Singh,  Phạm Văn Thiều và Phạm Việt Hùng biên dịch (Nhà xuất bản Trẻ)

* Năm 2000 giải được trao cho Laurent Lafforgue và Alain Connes về Công thức Vết [Trace formula] để giải các giả thuyết trong Chương trình Langlands [Langlands program].   

* Stanislav Smirnov và nhà nghiên cứu vật lý  Edward Witten nhận giải này trong năm 2001. 

* Năm 2002, có hai người nhận giải: Manindra Agrawal cùng hai sinh viên học với ông, thuộc Viện Kỹ thuật Ấn độ ở Kanpur [Indian Institute of Technology-Kanpur (IIT-K)] và Oded Schramm, thuộc công ty Microsoft. 

* Năm 2003, giải được trao cho  Richard Hamilton và Terrence Tao

* Năm 2004, giải được trao đồng thời cho Ben Green và cho Ngô Bảo Châu cùng đồng nghiệp là Gérard Laumon.  Ben Green ược giải về công cuộc nghiên cứu các nhóm số nguyên tố lập thành theo cấp số cộng (Progressions arithmétiques des nombres premiers = Arithmetic progressions of prime numbers). Gérad Laumon và Ngô bảo Châu nhận giải này với đề tài Le lemme fondamental pour les groupes unitaires(Fundamental Lemma for unitary groups = Bổ đề cơ bản cho các nhóm unita).

* Năm 2005, giải được trao đồng thời cho Manjul Bhargava, Nils Dencker

* Năm 2007, giải được trao đồng thời cho Alex Eskin, Christopher Hacon, Michael Harris, James McKernan, Richard Taylor

* Năm 2008, giải được trao đồng thời cho Cliff Taubes, Claire Voisin

* Năm 2009, giải được trao đồng thời cho Jean-Loup Waldspurger, Ian Agol, Danny Calegari và David Gabai

 

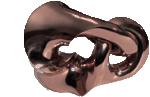
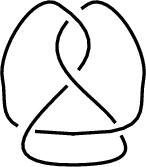
Giải này gồm một bản đúc bằng đồng sao lại tượng nguyên thủy bằng đá hoa cương. Phần bù của nút cấu hình số Tám  [Figure Eight Knot complement ] do nhà toán học kiêm điêu khắc gia Helaman Ferguson tạc thành cho CMI vào năm 1999. 

Ngoài ra, giải còn gồm hiện kim một triệu Mỹ kim.


 

           

 

2- Giải Thiên niên kỷ

            Ngoài giải Nghiên cứu được trao tặng hàng năm theo đề nghị của Hội đồng duyệt giải, Viện Toán Học Clay còn đưa ra giải thưởng Các bài Toán của Thiên niên kỷ [Millennium Prize Problems].  Giải này gồm bảy triệu Mỹ kim dành cho bài giải của bảy đầu đề toán học chưa có lời giải đáp đã được đặt ra từ nhiều năm trước đây.  Bảy đầu đề đã đuợc CMI lựa chọn là:

  1. Phỏng định của Poincaré
  2. Giả thuyết của Rieman: Bài toán thứ  8 chưa giải của Hilbert
  3. Phỏng định của Hodge liên quan đến đối đồng đều
  4. Bài toán của Stephen Cook, bài toán P đối NP, liên quan đến chiến lược phải chọn trước  một bài toán phức tạp và đối mặt với việc tìm giải pháp với sự kiểm nghiệm một giải pháp giả định.
  5. Những phương trình của Naviers-Stokes liên quan đến cơ học chất lỏng và sự đứng đắn của những nghiệm của phương trình đó
  6. Lý thuyết của Yang và Mills liên quan đến sự liên hệ giữa cơ học lượng tử và những không gian phần thớ
  7. Phỏng định của Birch Swinnerton-Dyer liên quan đến những đường cong ellip loại 1.

 

  • 1. La conjecture de Poincaré;
  • 2. L'hypothèse de Riemann : 8è problème, encore non résolu, de Hilbert;
  • 3. La conjecture de Hodge, portant sur la cohomologie;
  • 4. Le problème de Stephen Cook, P versus NP problem *, portant sur la stratégie à adopter face à un problème complexe et opposant la recherche de la solution à la vérification d'une solution présumée;
  • 5. Les équations de Navier-Stokes portant sur la mécanique des fluides et le bien fondé des solutions de ces équations;
  • 6. La théorie de Yang et Mills portant sur le lien entre la physique quantique et les espaces fibrés;
  • 7. La conjecture de Birch Swinnerton-Dyer portant sur les courbes elliptiques de genre 1.

* (P = polynomial time) và  (NP = nondeterministic polynomial time).

 
 

© http://vietsciences.free.fr , http://vietsciences.org   Trần Điển Ngọc