Première loi de Kepler

Jusqu'en 1609, les astronomes pensaient que les orbites des planètes étaient des combinaisons de cercles.
Mais Kepler, en étudiant les tables astronomiques établies par Tycho Brahe changea d'axe d'investigation : au lieu de supposer que les trajectoires des planètes étaient des combinaisons de cercles, il tenta de trouver une forme universelle d'orbites. Il a alors utilisé les positions de Mars relevées dans le ciel par Tycho Brahe, et Kepler comprend alors que ces orbites sont en fait des ellipses, dont le soleil occupe l'un des foyer.

Ainsi la première loi de Kepler s'énonce ainsi :

Les trajectoires des planètes sont des ellipses dont le Soleil occupe l'un des foyers.

L'ellipse

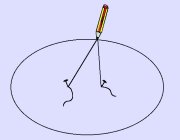
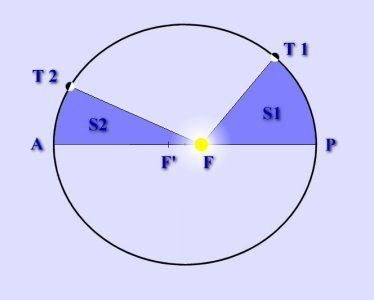
L'Aphélie est le point où la planète est la plus éloignée du soleil (et donc où sont mouvement est le plus lent comme nous allons le remarquer avec la deuxième loi de Kepler), et la Périhélie est le point où la planète est la plus proche du soleil;

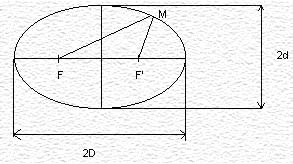
L'ellipse peut se définir de différentes manières. Elle peut tout d'abord être caractérisée de manière unique par les longueurs a et b, du demi petit axe et du demi grand axe. On remarque alors que si a=b, l'ellipse est particulière : c'est un cercle.

On a également contume de définir une ellipse en fonction de son excentricité et de son paramètre. L'excentricité d'une ellipse est le rapport de la distance d'un de ses foyer à son centre, sur la longueur a.
Ainsi, l'excentricité est un nombre entre 0 et 1. Plus l'excentricité devient faible, plus l'ellipse se rapproche du cercle, et plus l'excentricité est forte, plus l'ellipse est "aplatie".
Ainsi, les planètes connues du temps de Kepler (et avant) présentent une excentricité très faible, ce qui explique que les astronomes avaient considéré que l'orbites de ces planètes étaient des cercles, tout en remarquant certaines imprécisions apparentes, dont Kepler a tiré partie. (Il s'est servi de la planète Mars, d'excentricité 0.093, car Mercure d'excentricité 0.21 était difficilement observable, et Pluton n'était pas connue)

(Démonstration ici de l'impact de l'excentricité sur l'orbite, avec l'animation )

===================================================

Seconde Loi de Kepler

À quel point de son orbite elliptique une planète est - elle située à un moment donné? Dans 1609, Johannes Kepler a pu répondre à cette question avec la loi simple suivante:

Seconde Loi de Kepler sur le mouvement des planètes :
La ligne joignant la planète au soleil balaye des secteurs égaux dans des intervalles égaux de temps.

Les LOIS de KEPLER
bases de la mécanique céleste

	Première loi de KEPLER :
	*Les planètes tournent autour du Soleil en suivant des orbites en forme d'ellipse dont le Soleil occupe un des foyers.* Tous les corps en orbite autour du Soleil suivent cette loi. Les planètes ont en général des orbites peu excentriques, parfois même quasiment circulaire. Les comètes et certains astéroïdes, par contre, ont souvent des orbites elliptiques très excentriques (et donc très "aplaties"). Les satellites, qu'ils soient naturels ou artificiels, suivent aussi des orbites elliptiques "képlériennes". La Lune, le télescope spatial Hubble ou l'ISS, entre autres, sont satellites de la Terre. Leurs trois orbites ont un foyer commun, le centre de gravité de notre planète.
		Le trajet de la Terre autour du Soleil. F et F' : les deux foyers de l'ellipse. Le Soleil est en F. C : Centre géométrique de l'ellipse P : Périhélie (2 janvier) A : Aphélie (5 juillet) T : Terre Deux grandeurs définissent la forme de l'ellipse : son demi-grand axe : AC ou CP = a et son excentricité : e = CF / a pour la Terre, e=0,0017 et a=1 UA soit 149 597 870 km Les autres caractéristiques de l'ellipse en sont déduites. Demi-petit axe : Distance au périhélie : Rayon vecteur : où "v" est l'angle PFT.
	Un peu de géométrie à propos de l'ellipse. Une ellipse est une courbe plane fermée, possédant deux foyers. En sciant un tuyau rond en oblique, on génère une ellipse. L'ombre d'un objet plat et circulaire (pièce de monnaie, CD-ROM) présente facilement une forme elliptique. On peut définir complétement une ellipse en donnant seulement deux valeurs : la longueur de son demi-grand-axe (a) et son excentricité (e).
	Pour tracer une ellipse de demi-grand axe a et d'excentricité e, on peut utiliser une ficelle de longueur 2a fixée à deux punaises écartées de 2a fois e (les foyers F et F'). Tendez la ficelle avec un crayon et vous tracerez facilement l'ellipse. Lorsque les deux foyers sont confondus (cas de e=0), l'orbite est un cercle parfait (orbite circulaire), son excentricité est égale à zéro.

Deuxième loi de KEPLER, dite loi des aires :
*Les aires balayées par le rayon vecteur d'une planète sont proportionnelles au temps.* Le rayon vecteur est le segment de droite qui relie la planète au Soleil, sa longueur est variable. Les deux triangles curvilignes F-P-T1 et F-T2-A ont la même surface, soit S1 = S2. La 2ème loi de Képler implique que ces surfaces, étant égales entre elles, ont été balayées en des temps égaux. La planète a donc mis le même temps pour aller de P à T1 que pour aller de T2 à A. Comme on peut le constater, la distance P-T1 est plus grande, donc la vitesse moyenne sur ce trajet est plus élevée. La planète a donc une vitesse variable sur son orbite, suivant l'endroit de celle-ci où elle se trouve. Elle est plus élevée au périhélie (point P) qu'à l'aphélie (point A).
	La vitesse de la Terre autour du Soleil. S1 = S2 : les deux triangles curvilignes ont des surfaces égales. P : Périhélie (2 janvier) A : Aphélie (5 juillet) T1 et T2 : Deux positions de la Terre Les distance P-T1 et T2-A étant parcourues dans le même temps, les vitesses moyennes sur ces deux trajets sont différentes.
Troisième LOI DE KEPLER
*Pour toutes les orbites planétaires le rapport du carré des périodes de révolution (p) au cube du demi-grand-axe de l'orbite (a) est constant.* On peut exprimer a en Unités Astronomiques (en abrégé UA, 1 UA = 150 000 000 km) p en années K est une constante La troisième loi de KEPLER s'applique aussi, avec la même valeur de K, aux astéroïdes et aux comètes du système solaire. On peut l'appliquer à un ensemble de satellites orbitant autour d'une planète, comme Jupiter ou Saturne, entre autres, mais en redéfinissant la valeur de K pour chacun des systèmes. La troisième loi de KEPLER permet, connaissant la valeur de K et la période de révolution d'un astre, de calculer sa distance.

Les lois de Kepler

	Johannes Kepler fut l'assistant, puis le successeur de l'astronome Tycho Brahé. Il se servit des remarquables observations obtenues pour dégager les trois lois suivantes qui serviront de base à Isaac Newton pour établir sa théorie de la gravitation.
Johannes Kepler (1571 - 1630)		Tycho Brahé (1546 - 1601)

Première loi de Kepler (1609)

Rompant avec deux mille ans de dogme, Kepler annonce que les orbites décrites par les planètes ne sont pas des cercles mais des ellipses.
L'ellipse est la figure géométrique décrite par un point M d'un plan vérifiant la relation suivante par rapport à deux points donnés (les foyers) F et F' : MF + MF' = k (constante)

On définit également:

le demi-grand axe: D,
le demi-petit axe : d
la distance focale FF'
l'excentricité de l'ellipse e = FF'/2D

Deuxième loi de Kepler (1609)

Pour expliquer le phénomène dit "de préférence zodiacale" qui semblait indiquer des irrégularités dans la vitesse des astres autour du soleil, Kepler énonce la loi des aires

La deuxième loi de Kepler s'énonce ainsi :
La ligne qui relie la planète au Soleil balaie des aires égales pendant des temps égaux (voir ci-contre).
(Il s'écoule le même temps entre le passage de la planète entre A et B qu'entre C et D)

La troisième loi de Kepler (1619)

Kepler trouve la relation suivante entre la période sidérale T d'un astre et le demi-grand axe de son orbite :

T² (années) = a³ (Unités astronomiques)

Et leurs démonstrations....

Ces lois , empiriques, se révélaient très pratiques mais personne ne savait d'où elles provenaient...
En 1673, Christiaan Huygens démontra que l'expression de la force F nécessaire au maintien d'une planète sur une orbite circulaire autour d'un astre s'exprimait en 1/r².
En effet : l'expression de l'accélération dans le repère de Frenet est en v²/r (force centripète) pour un mouvement uniforme et circulaire.
D'après cette expression précédente et en se basant sur la troisième loi de Kepler pour une orbite circulaire de rayon r :
T² est proportionnel à r³ (dans le cas d'un cercle a = r : le demi-grand axe est égal au rayon)
Or T = 2pr/v donc T est proportionnel à r/v => r²/v² est proportionnel à r³ soit finalement en utilisant le principe fondamental de la dynamique dp/dt = F :

v² proportionnel à 1/r soit F proportionnel à 1/r²

Troisième loi de Kepler

Voici un tableau que Kepler aurait pu faire pour consigner les résultats des observations de Tycho Brahé et de ses calculs.

Pour les planètes du système solaire :

planète	a demi grand axe en 10³ km ou 10⁶ m	T période de révolution en jour	T période de révolution en 10⁶ s	T²/a³ en jour².km^-3	T²/a³ en s².m^-3
Mercure	57910	87,97	7,57984708	3,98482.10^-11	2,95842.10^-19
Vénus	108200	224,7	19,3610508	3,98588.10^-11	2,95921.10^-19
Terre	149600	365,26	31,47226264	3,98483.10^-11	2,95843.10^-19
Mars	227940	686,98	59,19294472	3,98498.10^-11	2,95855.10^-19
Jupiter	778330	4332,71	373,3236244	3,98133.10^-11	2,95583.10^-19

Pour les satellites de Jupiter observés par Galilée :

satellite	a demi grand axe en 10³ km ou 10⁶ m	T période de révolution en jour	T période de révolution en 10⁶ s	T²/a³ en jour².km^-3	T²/a³ en s².m^-3
Io	422	1,77	0,15251028	4,16878.10^-8	3,095.10^-16
Europe	671	3,55	0,3058822	4,17147.10^-8	3,097.10^-16
Ganymède	1070	7,15	0,6160726	4,17312.10^-8	3,09822.10^-16
Callisto	1883	16,69	1,43807716	4,17217.10^-8	3,09751.10^-16

On observe bien que T²/a³ est une constante mais que cette constante dépend de l’astre attracteur.

On a T²/a³ = 4p ²/GM, où G est la constante de gravitation universelle : G = 6,67.10^-11 m³.kg^-1.s^-2

En prenant en compte les résultas des tableaux ci-dessus, il est donc possible de déterminer la masse des astres. On trouve par exemple :

pour le Soleil :M_S = 2,00.10³⁰ kg
pour Jupiter :M_J = 1,91.10²⁷ kg

Les lois de Kepler s’appliquent aussi bien aux satellites naturels qu’aux satellites artificiels d’un astre.

Pour quelques satellites de la Terre :

satellite	a demi grand axe en 10³ km ou 10⁶ m	T période de révolution	T période de révolution en s	T²/a³ en s².m^-3
Lune	384	27,32 jours	2,35.10⁶	9,78632.10^-14
Hipparcos	24,546	10h37min 57s	38277	9,9068.10^-14
NOAA 15	7,19	1h41min09s	6069	9,90941.10^-14
GPS BII-01	26,5625	11h58min08s	43088	9,90617.10^-14
Globalstar MO48	7,79	1h54min4s	6844	9,90849.10^-14

En utilisant la constante trouvée pour les satellites artificiels (quatre dernières lignes du tableau) on obtient comme masse de la terre M_T = 5,97.10²⁴ kg

La constante obtenue avec la Lune est légèrement différente. Newton a déjà corrigé la troisième loi de Kepler en montrant que la masse qui intervenait était en fait la somme des masses des deux corps en interaction gravitationnelle (ici la Terre et la Lune).

En se servant de la correction de Newton on trouve M_{Terre + Lune} = 6,05.10²⁴ kg et par différence la masse de la Lune est M_L = 7,36.10²² kg.

En fait, la troisième loi n’est qu' approchée et les bons résultats obtenus par Kepler sont dus au fait que la masse des planètes est négligeable devant celle du Soleil (Jupiter, la plus grosse planète a une masse qui ne dépasse pas le millième de celle du Soleil).

Les aires balayées par le rayon vecteur d'une planète sont proportionnelles au temps.

Le rayon vecteur est le segment de droite qui relie la planète au Soleil, sa longueur est variable.
Les deux triangles curvilignes F-P-T1 et F-T2-A ont la même surface, soit S1 = S2.
La 2ème loi de Képler implique que ces surfaces, étant égales entre elles, ont été balayées en des temps égaux.
La planète a donc mis le même temps pour aller de P à T1 que pour aller de T2 à A. Comme on peut le constater, la distance P-T1 est plus grande, donc la vitesse moyenne sur ce trajet est plus élevée.
La planète a donc une vitesse variable sur son orbite, suivant l'endroit de celle-ci où elle se trouve. Elle est plus élevée au périhélie (point P) qu'à l'aphélie (point A).


	La vitesse de la Terre autour du Soleil. S1 = S2 : les deux triangles curvilignes ont des surfaces égales. P : Périhélie (2 janvier) A : Aphélie (5 juillet) T1 et T2 : Deux positions de la Terre Les distance P-T1 et T2-A étant parcourues dans le même temps, les vitesses moyennes sur ces deux trajets sont différentes.
Troisième LOI DE KEPLER
*Pour toutes les orbites planétaires le rapport du carré des périodes de révolution (p) au cube du demi-grand-axe de l'orbite (a) est constant.* On peut exprimer a en Unités Astronomiques (en abrégé UA, 1 UA = 150 000 000 km) p en années K est une constante La troisième loi de KEPLER s'applique aussi, avec la même valeur de K, aux astéroïdes et aux comètes du système solaire. On peut l'appliquer à un ensemble de satellites orbitant autour d'une planète, comme Jupiter ou Saturne, entre autres, mais en redéfinissant la valeur de K pour chacun des systèmes. La troisième loi de KEPLER permet, connaissant la valeur de K et la période de révolution d'un astre, de calculer sa distance.