|
Dao
động là một dạng chuyển động
rất thường gặp trong đời
sống, trong kỹ thuật. Thí dụ: dao động
của con lắc đồng hồ, dao động
của cầu khi xe lửa chạy qua, dao động
của ḍng điện trong mạch... Nói một cách
tổng quát, dao động là một chuyển
động được lặp lại nhiều
lần theo thời gian. Quan sát một hệ dao
động, một con lắc chẳng hạn, ta
thấy nó có những tính chất tổng quát
sau:
a.
Hệ phải có một vị trí cân bằng
bền và hệ dao động qua lại hai bên
vị trí đó.
b.
Khi hệ rời khỏi vị trí cân bằng
bền, luôn luôn có một lực kéo hệ
về vị trí cân bằng bền gọi là
lực hồi phục.
c.
Hệ có quán tính: khi chuyển đến vị
trí cân bằng, do quán tính, nó tiếp tục vượt
qua vị trí cân bằng đó.
Trong
chương này chúng ta chỉ nghiên cứu các dao
động cơ.
|
1. Hiện tượng |

|
|
2. Phương tŕnh dao động điều
ḥa
|

|
Dưới
đây, chúng ta thiết lập phương tŕnh
dao động điều ḥa, cụ thể là t́m
sự phụ thuộc của độ dời x
của con lắc ḷ xo theo thời gian. Viết phương
tŕnh của định luật 2 Newton đối
với quả cầu ta có:
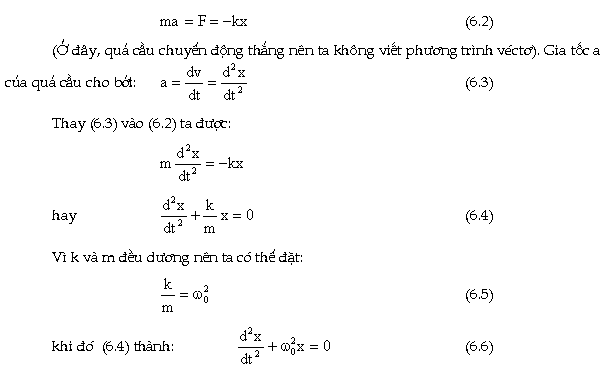
Ta
được một phương tŕnh vi phân
của x gọi là phương tŕnh vi phân của
dao động điều ḥa. Đây là một phương
tŕnh vi phân cấp hai thuần nhất, hệ
số không đổi. Theo giải tích, nghiệm
của nó có dạng:

|
3. Khảo sát dao động điều ḥa
|

|
Phương
tŕnh (6.7) cho ta độ dời x của con
lắc ḷ xo tại một thời điểm t.
Đại lượng A được gọi là biên
độ dao động, rơ ràng là:

Quả
vậy, dễ dàng nghiệm lại các hệ
thức sau:
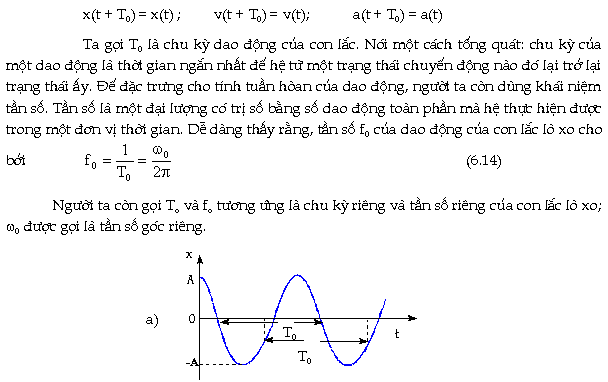
H́nh
6.2 a Biểu diễn đồ
thị của x theo thời gian t
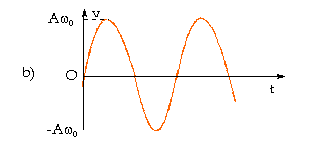
H́nh
6.2b Biểu diễn đồ thị của v theo
thời gian t.
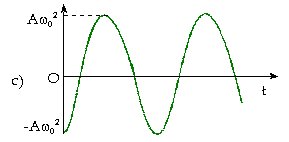
H́nh
6.2 c Biểu diễn đồ thị của a
theo thời gian t.
|
4. Năng lượng dao động điều
ḥa
|

|
Ta
hăy tính năng lượng dao động điều
ḥa của con lắc ḷ xo. Dao động là
một dạng chuyển động cơ, v́
vậy năng lượng dao động là cơ
năng W cho bởi:
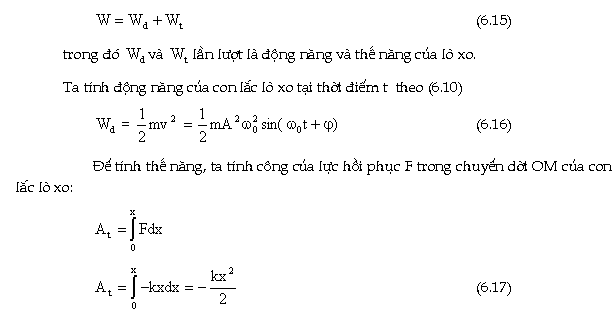
Công
đó bằng độ biến thiên
thế năng của con lắc ḷ xo từ O
đến M

Đó
là biểu thức năng lượng của
hệ dao động điều ḥa, năng lượng
được bảo toàn trong quá tŕnh dao động.
Điều này phù hợp với định luật
bảo toàn cơ năng. Trong quá tŕnh dao động
điều ḥa, cơ năng, tức là tổng
động năng và thế năng, bảo toàn,
nhưng luôn luôn có sự chuyển ḥá giữa
động năng và thế năng. Từ (6.20)
ta có thể suy ra:

Công
thức này cho phép ta tính tần số riêng (0 khi
biết A, m và W. Những kết quả trên đây
tuy được suy từ
dao động điều ḥa của con
lắc ḷ xo nhưng cũng đúng đối
với một hệ bất kỳ dao động
điều ḥa .
|
5. Con lắc
|

|

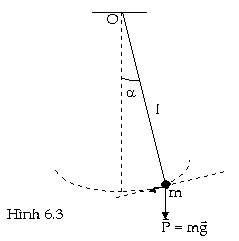
Trong
vật lư, người ta hiểu con lắc là
một vật rắn thực hiện dao động
xung quanh một điểm hay một trục
cố định dưới tác dụng của
trọng lực. Người ta thường phân
biệt con lắc toán học và con lắc vật
lư. Con lắc toán học là một hệ
được lư tưởng hóa gồm một
sợi dây không trọng lượng và không dăn
treo một khối lượng được
tập trung vào một điểm. Một quả
cầu nặng không lớn treo vào một sợi
dây mảnh dài một cách gần đúng, có
thể xem như con lắc toán học. Độ
lệch của con lắc khỏi vị trí cân
bằng được đặc trưng bởi
góc lệch ( tạo bởi sợi dây với
đường thẳng đứng (h́nh 6.3)
Khi con
lắc lệch khỏi vị trí cân bằng
sẽ xuất hiện momen
lực M,
về độ lớn bằng mglsin( (m là
khối lượng, c̣n l là độ dài con
lắc). M có tác dụng đưa con lắc
trở về vị trí cân bằng, vậy tác
dụng của nó tương tự như lực
đàn hồi của con lắc ḷ xo.

Dấu
trừ được đưa vào ở đây
để tính đến tác dụng của
Mômen M có xu hướng đưa m về vị
trí cân bằng có thể đưa phương tŕnh
này về dạng

Do
đó, với các dao động bé, độ
lệch góc của con lắc toán học biến
đổi với thời gian theo định
luật điều ḥa .
Từ
(6.24), ta thấy tần số dao động
của con lắc toán học chỉ phụ
thuộc vào độ dài của con lắc và vào
gia tốc trọng trường mà không phụ
thuộc vào khối lượng con lắc. Theo công
thức (6.24) ta thu được biểu thức
của chu kỳ dao động của con lắc
toán học:

Nếu
không thể biểu diễn vật dao động
như một chất điểm th́ con lắc
được gọi là con lắc vật lư. Khi
con lắc lệch khỏi vị trí cân bằng
một góc ( sẽ xuất hiện một momen
lực có xu hướng làm con lắc quay về
vị trí cân bằng. Momen này bằng:

trong
đó m là khối lượng của con lắc,
c̣n l là khoảng cách giữa điểm treo O và
khối tâm C của con lắc (h́nh 6.4)
Nếu
kư hiệu momen quán tính của con lắc đối
với trục đi qua điểm treo bằng
chữ́ I th́ có thể viết:

Trong
trường hợp các dao động bé (6.29)
chuyển về phương tŕnh mà ta đă
biết:

Từ
các phương tŕnh (6.30) và (6.31) suy ra rằng
với các độ lệch nhỏ khỏi
vị trí cân bằng, con lắc vật lư
thực hiện các dao động điều ḥa
có tần số phụ thuộc vào khối lượng
của con lắc, vào momen quán tính của con
lắc đối với trục quay và vào kḥảng
cách giữa trục quay và khối tâm của con
lắc. Theo (6.31) chu kỳ dao động của
con lắc vật lư được xác định
bằng biểu thức:

So
sánh các công
thức (6.27) và (6.32) ta thấy nếu
con lắc toán học có
độ dài:

th́
nó có chu kỳ dao động giống như con
lắc vật lư vừa xét. Ta gọi đại
lượng (6.33) là độ dài rút gọn
của con lắc vật lư. Vậy độ dài
rút gọn của con lắc vật lư là độ
dài của một con lắc toán học có chu
kỳ dao động trùng với chu kỳ của
con lắc vật lư đă cho.
Một
điểm nằm trên đường thẳng
đi qua điểm
treo với khối tâm, nằm cách trục quay
một kḥảng bằng độ dài rút gọn
được gọi là tâm đu đưa
của con lắc vật lư (xem điểm O' trên
h́nh 6.4).

|
1. Hiện tượng
|

|
Trong
thực tế, khi khảo sát dao động
của một hệ, ta không thể bỏ qua các
lực ma sát. Do có ma sát, năng lượng
của hệ dao động giảm dần theo
thời gian v́ theo (6.20) biên độ dao động
là giảm dần theo thời gian. Dao động
của hệ sẽ là dao động tắt
dần. Xét một hệ dao động chịu tác
dụng của lực cản của môi trường
(lực nhớt); Nếu vận tốc dao động
của hệ nhỏ th́ thực nghiệm
chứng tỏ vật cản của môi trường
ngược chiều và tỉ lệ với
vận tốc của hệ. Tức là:

|
2. Phương tŕnh dao động tắt
dần
|

|
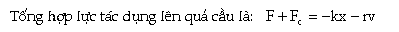
Viết
phương tŕnh của định luật 2
Newton đối với quả cầu ta được:
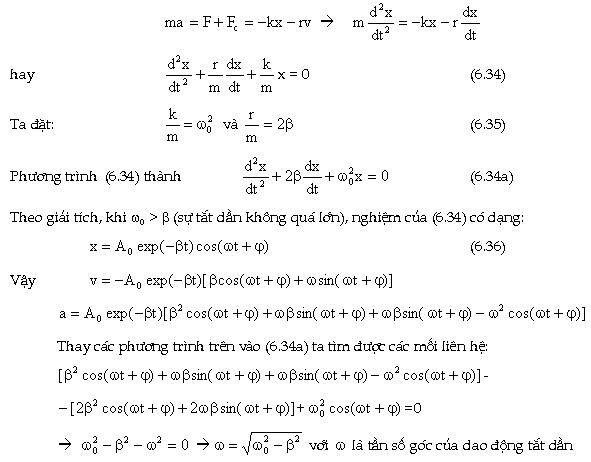
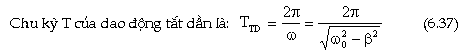
|
3. Khảo sát dao động tắt dần
|

|
Trong
dao động tắt dần, biên độ không
c̣n là hằng số mà giảm dần theo
thời gian theo hàm mũ:
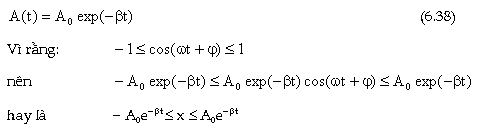
Như
vậy đồ
thị của x theo t là một đường
cong nội tiếp giữa hai đường cong
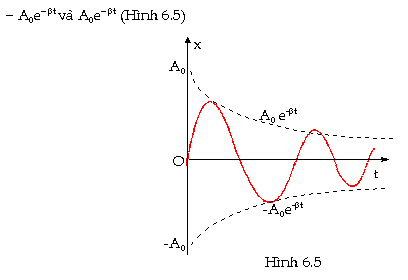

Biên
độ dao động giảm là v́ năng lượng
của hệ trong quá tŕnh dao động giảm
dần để chuyển thành công chống
lại công của lực cản.

| III.
DAO ĐỘNG CƠ CƯỠNG BỨC
|
|
|
1. Hiện tượng
|

|
Giả
sử ta cung cấp năng lượng liên
tục cho hệ dao động để bù
lại những phần năng lượng đă
giảm để sinh công thắng công của
lực ma sát th́ dao động của hệ
sẽ không tắt dần nữa, dao động
của hệ sẽ được duy tŕ.
Việc cung cấp năng lượng liên tục
cho hệ có thể thực hiện được
bằng cách tác dụng lên hệ một ngoại
lực. Công do lực này sinh ra sẽ có trị
số bằng phần năng lượng bù đắp
cho hệ. Muốn cho hệ tiếp tục dao
động, ngoại lực tác dụng phải
biến thiên tuần ḥan theo thời gian. Dao động
mà hệ thực hiện dưới tác dụng
của ngoại lực tuần ḥan gọi là dao
động cưỡng bức.
Khi
tác dụng ngoại lực tuần ḥan lên
hệ, hệ bắt đầu dao động.
Thực nghiệm chứng tỏ rằng trong giai
đoạn đầu, dao động của
hệ khá phức tạp. Nó là chồng chất
của hai dao động: dao động riêng
tắt dần dưới tác dụng của
nội lực và dao động cưỡng
bức dưới tác dụng của ngoại
lực tuần ḥan. Sau một thời gian đủ
lớn (gọi là thời gian quá độ), dao
động tắt dần coi như không c̣n
nữa; khi đó dao động của hệ
chỉ là dao động cưỡng bức dưới
tác dụng của ngoại lực tuần ḥan.
Thực nghiệm cũng chứng tỏ rằng
dao động cưỡng bức có chu kỳ
bằng chu kỳ của ngoại lực tuần ḥan
tác dụng.
|
2. Phương tŕnh dao động cưỡng
bức |

|
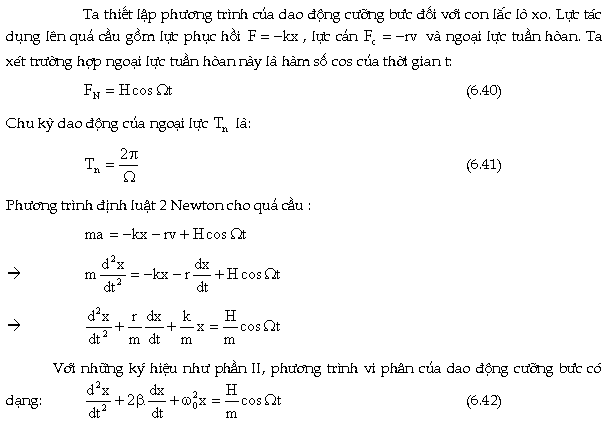

Vậy
ta có hai phương tŕnh:
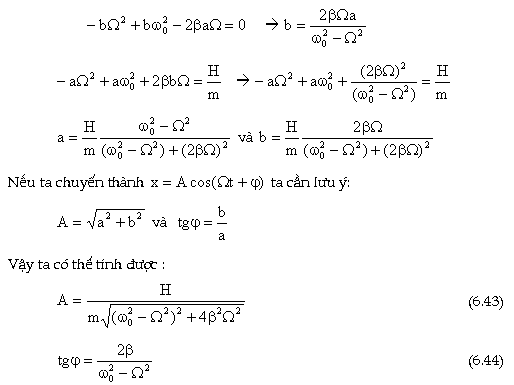
|
3. Khảo sát dao động cưỡng
bức. Cộng hưởng
|

|
Trước
hết, ta nhận thấy rằng biên độ A
và pha ban đầu ( của dao động cưỡng
bức đều phụ thuộc tần số góc
( của ngoại lực tác dụng. Nghiên cứu
sự phụ thuộc của biên độ A theo
ta được kết quả sau :

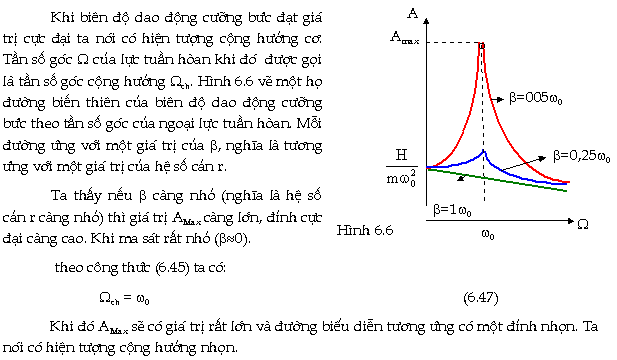
|
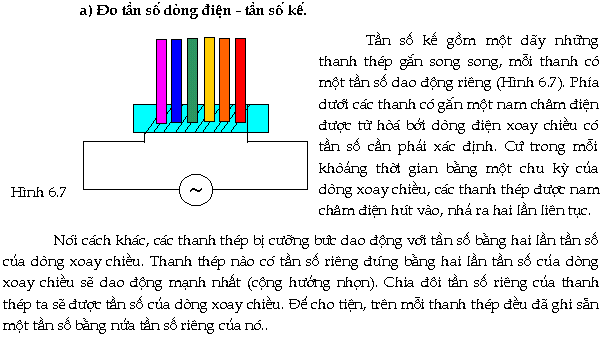
4. Ứng dụng của hiện tượng
cộng hưởng cơ
|

|
Các
ứng dụng tŕnh bày sau đây cho ta thấy rơ
tác dụng của hiện tượng cộng hưởng
cơ, đặc biệt là hiện tượng
cộng hưởng nhọn.
b)
Ngăn ngừa sự phá ḥại v́ cộng hưởng
cơ.
Trong
thực tế, hiện tượng cộng hưởng
cơ thường gây nhiều tác hại. Cầu
bắc qua sông, đặc biệt là cầu treo,
bao giờ cũng có một tần số dao động
riêng. Nếu cầu chịu
một lực tác dụng tuần ḥan có tần
số xấp xỉ tần số riêng của nó,
cầu có thể rung động rất mạnh và
có thể bị găy.
Dưới
đây ta xét trường hợp nguy hiểm có
thể xảy ra khi có một động cơ
quay đặt trên một nền xi măng (H́nh
6.8). Khi động cơ quay, nền xi măng rung
động. Ứïng với một tần số
quay nào đó của động cơ, nền xi măng
có thể rung động mạnh nhất và có
thể bị phá vỡ. Nguyên nhân là v́ các
bộ phận quay của động cơ không
thể nào làm ḥan toàn đối xứng
được, nên trọng tâm của các bộ
phận này không nằm trên trục quay. Khi động
cơ quay, các bộ phận này sinh ra một
lực kích thích tuần ḥan tác dụng lên
trục máy và nền xi măng. Ứng với
một vận tốc góc quay nào đó của
động cơ mà tần
số góc của lực kích thích bằng tần
số riêng của động cơ
th́ sẽ xảy ra hiện tượng
cộng hưởng nhọn và nền xi măng có
thể bị phá vỡ, trục động cơ
có thể bị găy. Vận tốc góc đó
của động cơ gọi là vận tốc
nguy hiểm.

TRỌNG
TẬM ÔN TẬP
***@@@***
1-
Nghiệm của phương tŕnh dao động
điều ḥa.
2-
Liên hệ giữa tần số góc, tần
số, chu kỳ T đối với dao động
của ḷ xo và dao động của con lắc.
3-
Năng lượng của dao động
điều ḥa.
4-
Nghiệm của phương tŕnh dao động
tắt dần, tần số, biên độ,
giảm lượng Loga.
5-
Dao động cưỡng bức, điều
kiện để có cộng hưởng, lợi
ích và tác hại của cộng hưởng.
BÀI
TẬP
***&&&***
1.
Một chất điểm có khối lượng
500 g, dao động điều ḥa với tần
số f=2 Hz. Biên độ dao động là 5 cm. Xác
định vận tốc, gia tốc của
chất điểm. Xác định lực tác
dụng lên chất điểm tại vị trí cách
vị trí cân bằng 2,5 cm.
2.
Biên độ dao động của con
lắc là 50, khối lượng quả nặng là
500g, chu kỳ con lắc là 2 giây. Do có ma sát mà sau
5 chu kỳ dao động biên độ dao động
chỉ c̣n 40. Dao động được duy tŕ
nhờ bộ máy của đồng hồ. Tính công
suất của máy đó.
3.
T́m sự biến
thiên chu kỳ của một con lắc toán
học gồm một dây kim loại bị co dăn
theo sự thay đổi nhiệt độ (t
=t2-t1. T́m sự biến
thiên chu kỳ của con lắc nói trên theo sự
thay đổi độ cao so với mặt đất.
4.
T́m giảm lượng loga của sự dao
động tắt dần trên điện nảo
đồ của một bịnh nhân. Cho biết
cứ sau thời gian 5 phút th́ cơ năng toàn
phần của dao động giảm 4.104 lần.
Cho biết chu kỳ của dao động là T= 0,5
giây.
5.
Một dao động tắt dần của
một điểm xảy ra theo qui luật x=A0 e-(t
sin (t. Trong đó A0, (, ( là các hằng số dương.
T́m:
a) Biên độ dao động và vận
tốc của điểm đó tại thời
điểm t =0 .
b) Biên độ dao động và vận
tốc của điểm đó ở các thời
điểm khi điểm đó dịch chuyển
đến các vị trí bờ.
- Dưới
tác dụng của một ngoại lực
thẳng đứng F=F0 cos(t, một vật treo
trên một ḷ xo thực hiện những dao
động cưởng bức theo qui luật
x=A0cos((t-a). T́m công của lực F sau một
chu kỳ dao động. Chứng tỏ
rằng công nầy dùng để thắng
lực ma sát.
CÂU
HỎI TRẮC NGHIỆM
***@@@***
- Năng
lượng của con lắc ḷ xo gắn
với quả nặng th́ tỷ lệ với
:
a)
Biên độ dao động.
b)
B́nh phương khối lượng quả
nặng.
c)
B́nh phương của tần số.
d) B́nh phương biên độ và độ
cứng ḷ xo.
- Hai
con lắc ḷ xo có cùng độ cứng K.
Biết tần số dao động f1 =2 f2
Vậy hai khối lượng sẽ liên
hệ theo công thức:
a)
M1 =
M2/4
b) M1 = M2/2
c) M1 = M2/
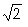
d)
M1 = 4 M2
e) M1 = 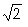 M2
M2
- Hai
con lắc có cùng độ dài và cùng biên
độ dao
động. Nếu M1 = 2 M2 th́ :
a)
Chu kỳ và năng lượng của hai con
lắc là bằng nhau.
b)
Chu kỳ T1 =T2/2 và năng lượng của hai
con lắc là bằng nhau.
c)
Chu kỳ T1 =T2 và năng lượng E1 lớn hơn
năng lượng E2.
d)
Chu kỳ T1 =T2 và năng lượng E1 nhỏ hơn
năng lượng E2.
- Khi
độ dài của một con lắc
đơn tăng
lên gấp đôi, th́ tỉ số tần
số của nó lúc sau so với lúc đầu
là:
a)
2
b) 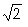 c)
1/
c)
1/ 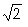 d) 1/4
e) 1
d) 1/4
e) 1
- Một
con lắc toán học dao động tắt
dần với chu kỳ T. Nếu đặt
trong thang máy đang đi lên nhanh dần
với gia tốc g/2 th́:
a)
Giảm
lượng loga tăng.
b) Giảm
lượng loga giảm.
c)
Giảm lượng loga không đổi.
d)
Biên độ tăng lên.
e)
Biên độ không thay đổi.
- Khi
một dao động có tần số tăng lên
gấp 3 và biên độ giảm 2 lần th́
tỷ số năng lượng của con
lắc so với lúc đầu:
a)
9/4
b) 4/9
c) 3/2
d) 2/3
e)
1
PHÂN
TÍCH NHỮNG CÂU PHÁT BIỂU ĐÚNG SAI
***@@@***
1-
Có hai ḷ xo giống nhau được
nối với một quả cầu tạo thành
con lắc. Khi mắc hai ḷ xo song song th́ chu kỳ
dao động sẽ lớn hơn khi mắc hai ḷ
xo nối tiếp.
2-
Một con lắc toán học đặt vào
trong thang máy, khi thang máy đi xuống nhanh dần
với gia tốc a th́ tần số dao động
sẽ tăng lên.
3-
Khi tần số ngoại lực tác dụng
lên hệ dao động là không đổi th́ biên
độ của một dao động cưởng
bức đạt cực đại.
4-
Khi một con lắc toán học đang dao
động, tại các vị trí biên th́ lực căng
dây là lớn nhất.
5-
Cộng hưởng và cưỡng bức luôn
đi đôi với nhau.


|