|
Vật
rắn có thể xem như một hệ chất
điểm. Nếu sự biến dạng của
vật khi tương tác với các vật khác là
nhỏ, bỏ qua được thì ta có thể
coi vật là vật rắn tuyệt đối.
Vật rắn tuyệt đối là vật mà
khoảng cách giữa hai điểm bất kỳ
của nó không đổi. Nói cách khác, hình
dạng của vật rắn không thay đổi
trong quá trình chuyển động của nó.
Vật rắn tuyệt đối thường
được xem là hệ chất điểm liên
kết chặt chẻ với nhau.
Chuyển
động của vật rắn được xác
định bởi các ngoại lực đặt
vào nó. Một chuyển động phức
tạp của vật rắn có thể phân tích thành
hai dạng chuyển động: chuyển động
với quỹ đạo thẳng gọi là
chuyển động tịnh tiến và chuyển
động quay. Chuyển động tịnh
tiến là chuyển động mà quỹ đạo
mọi chất điểm trong vật rắn là
những đường thẳng song song với
nhau.
Phương
trình chuyển động tịnh tiến của
vật rắn được rút ra từ
đinh luật 2 Newton viết cho toàn bộ các
chất điểm mi của cả hệ có liên
quan đến khối tâm C của hệ dưới
dạng phương trình (4.7) ở chương 4.
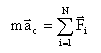
Như
vậy, dù vật rắn có chuyển động
bất kỳ thì khối tâm của nó cũìng
chuyển động giống như một
chất điểm có khối lượng
bằng khối lượng của cả vật
rắn và chịu
sự tác dụng của tổng tất cả các
ngoại lực đặt vào vật rắn.
| I.
CHUYỂN ÐỘNG QUAY CỦA VẬT
RẮN QUANH MỘT TRỤC
|
|
|
1. Nhận xét
|

|
Khi
vật rắn quay quanh một trục ( (nằm
trong hay nằm ngoài vật rắn đó) thì
mọi chất điểm mi trên vật rắn
đều quay quanh trục ( với cùng một
vận tốc góc ( như nhau đồng thời
có quỹ đạo là những đường
tròn nằm trong mặt phẳng vuông góc với
trục quay. Tâm 0 của các vòng tròn đó
nằm ngay trên trục quay. Bán kính ri tính từ
mi đến trục quay 0 thường là khác nhau
vì vị trí của các chất điểm là khác
nhau.
Muốn vật rắn quay được, ta
phải tác dụng lực lên vật rắn đó.
Muốn lực đó có khả năng làm quay
vật thì lực đó không thể song song
với trục quay mặc khác nó cũng không
thể có giá đi qua trục quay.
Ðể
xét khả năng của lực làm quay một
vật quanh một trục ta xét ví dụ sau:
Một cánh cửa có thể quay quanh một
trục thẳng đứng xuyên qua các bản
lề. Lấy tay ấn vào cửa ở gần
trục quay thì ta thấy rằng phải ấn khá
mạnh mới đẩy được cửa.
Trái lại, nếu ấn vào cửa ở một
chổ khá xa trục quay thì ta có thể đẩy
cửa một cách dễ dàng. Ðiều này
chứng tỏ rằng khả năng làm quay
vật của một lực phụ thuộc độ
lớn của lực và phụ thuộc vào
khoảng cách giữa điểm đặt
của lực đến trục quay (ta gọi
đó là cánh tay đòn). Khả năng của
lực làm quay một vật quanh một trục
được đặc trưng bởi một
đại lượng gọi là mômen lực
đối với trục quay ấy.
|
2. Mômen lực đối với một
trục |

|

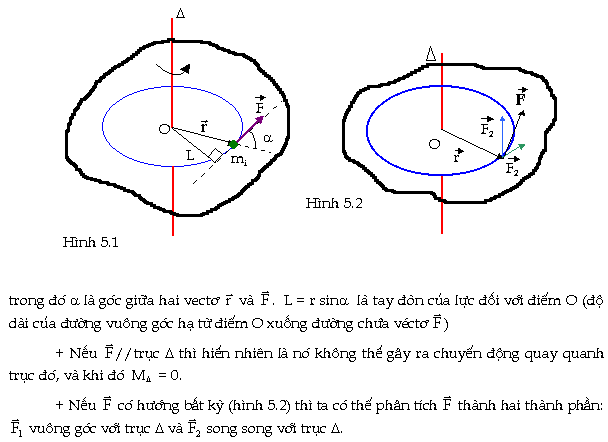
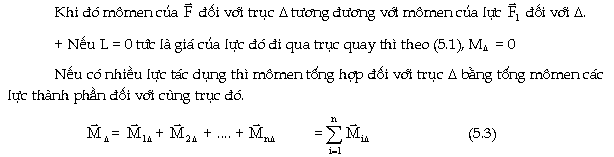
+
Mômen tổng hợp của các nội lực
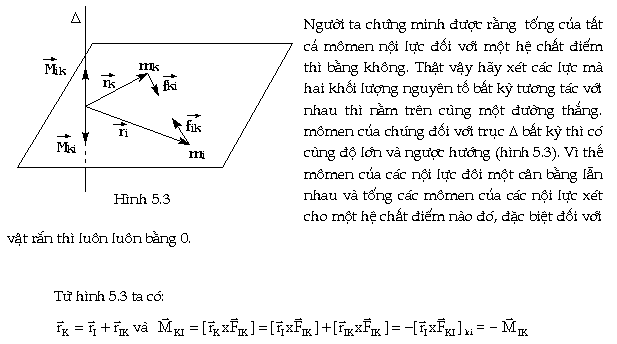
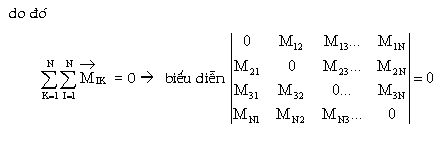
| II.
PHƯƠNG TRÌNH ÐỘNG LỰC HỌC CƠ
BẢN CỦA CHUYỂN ÐỘNG QUAY
|

|

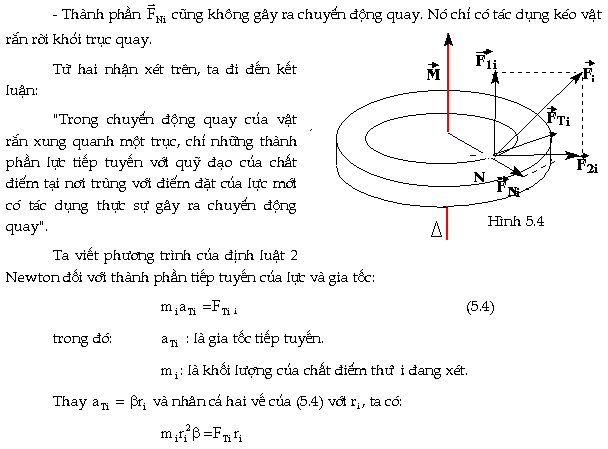


Phương
trình (5.10) được gọi là phương trình
động lực học cơ bản của
chuyển động quay. Nó có dạng giống như
phương trình của định luật 2
Newton.
Ðem
so sánh ta thấy trong chuyển động quay mômen
lực đóng vai trò của lực, mômen quán tính
đóng vai trò của khối lượng và gia
tốc góc đóng vai trò của gia tốc dài.
Từ
đó ta thấy mômen quán tính của vật là
số đo mức quán tính của vật trong
chuyển động quay.

Khái
niệm mômen lực và mômen quán tính là dựa trên
cơ sở sự quay của vật rắn. Tuy
nhiên, các đại lượng đó tồn
tại không phụ thuộc vào sự quay.
Chẳng hạn, một vật bất kỳ, quay
hay đứng yên, đều có mômen quán tính xác
định đối với một trục
bất kỳ cũng giống như vật có
khối lượng không tuỳ thuộc vào
trạng thái chuyển động hay đứng yên
của vật. Momen lực đối với
một trục ( bất kỳ cũng tồn
tại độc lập đối với trường
hợp vật quay quanh trục ( đó hay là đứng
yên. Trong trường hợp vật đứng yên,
mômen của lực xét đã được cân
bằng bởi mômen của các lực khác tác
dụng trên vật.
|
1.
Mật độ khối lượng
|

|
Từ
(5.9) ta thấy rằng mômen quán tính là đại
lượng có tính cộng được tức
là mômen quán tính của vật là tổng các mômen
quán tính của các phần tử tạo nên
vật.
Sự
phân bố khối lượng trong các giới
hạn của vật có thể được
đặt trưng bởi một đại lượng
gọi là mật độ khối lượng,

Nếu
vật có dạng đường
thì biểu thức mật độ là :
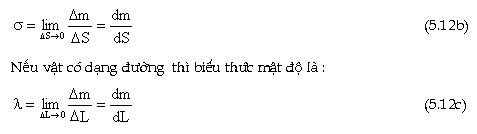
|
2.
Biểu thức của mômen quán tính
|

|
a)
Trường hợp trục quay đi qua khối tâm.

b)
Tính mômen quán tính.
Ta
hãy áp dụng biểu thức (5.15) để xác
định mômen quán tính của một số
vật rắn.

Xét
một hình trụ thẳng, tiết diện tròn bán
kính R, chiều cao h. Hãy tính mômen quán tính đối
với trục đối xứng. Giả
thiết hình trụ đồng chất. Khi đó
trục đối xứng của hình trụ cũng
là trục đối xứng vật chất
của nó. Chia hình trụ thành những lớp
trụ mỏng, bán kính trong r, bán kính ngoài r + dr
(hình 5.5).
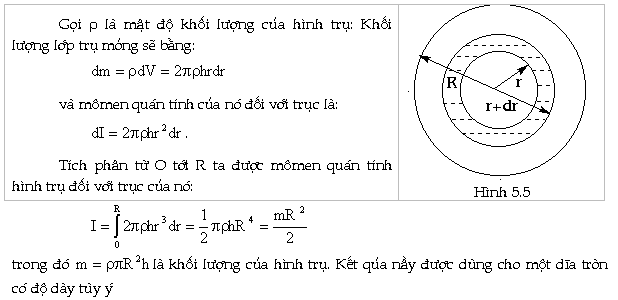
Xét
một quả cầu đồng chất, có
khối lượng m và bán kính R. Tính mômen quán tính
của quả cầu đối với trục z
đi qua tâm O.
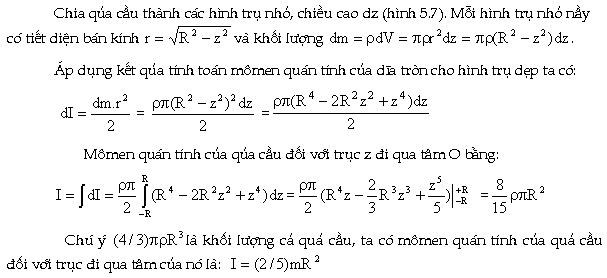
c)
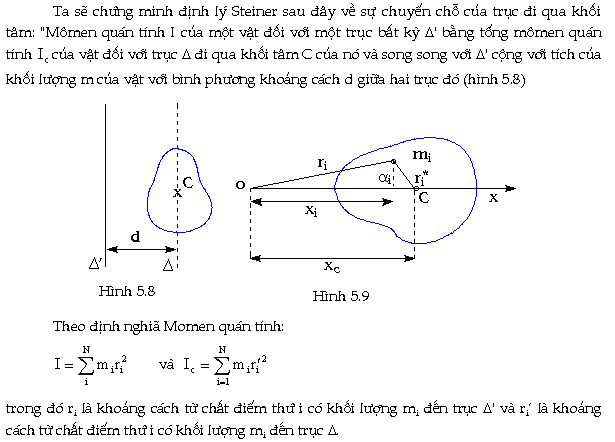
Trường hợp trục quay song song với
trục đi qua khối tâm
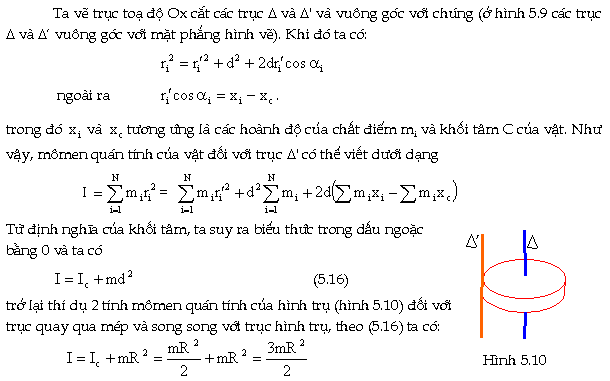
d ) Thứ nguyên và đơn vị của mômen quán
tính.
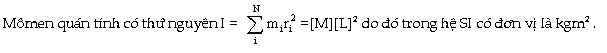
e)
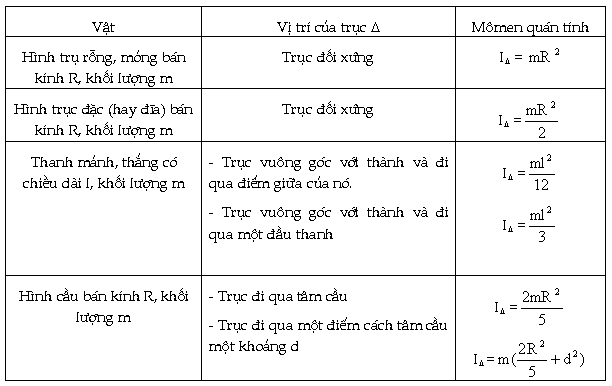
Bảng ghi công thức tính mômen quán tính của
một vài vật đồng chất
|
1. Vật rắn quay xung quanh một trục
cố định |

|
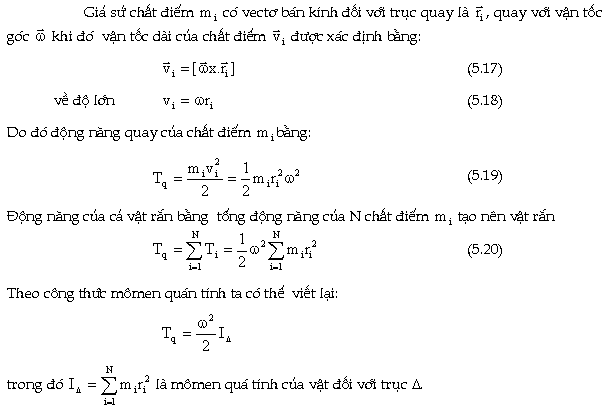

|
2.
Vật rắn trong trường hợp
chuyển động tổng quát
|

|
Khi
vật rắn chuyển động phức
tạp ta có thể phân tích chuyển động
của vật rắn thành hai chuyển động:
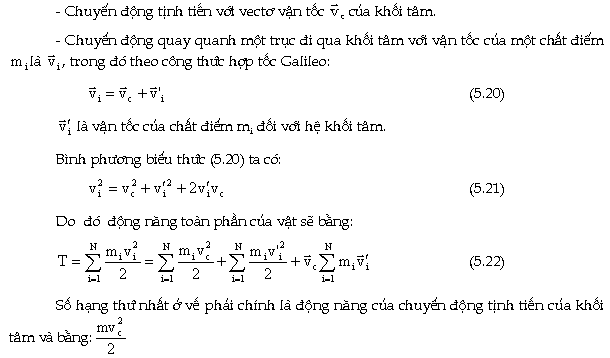
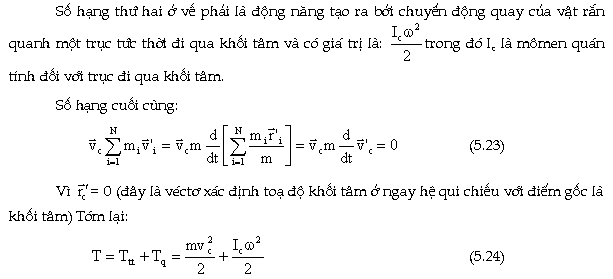
Như
vậy chúng ta đã chứng minh định lý
sau:
"Ðộng
năng toàn phần của vật rắn bằng
tổng động năng tịnh tiến của
khối tâm mang khối lượng của cả
vật và động năng quay của nó xung
quanh trục đi qua khối tâm".
| V.
MÔMEN XUNG LƯỢNG-SỰ
BẢO TOÀN MÔMEN XUNG LƯỢNG
|
|
|
1.Mômen xung lượng của một
chất điểm |

|
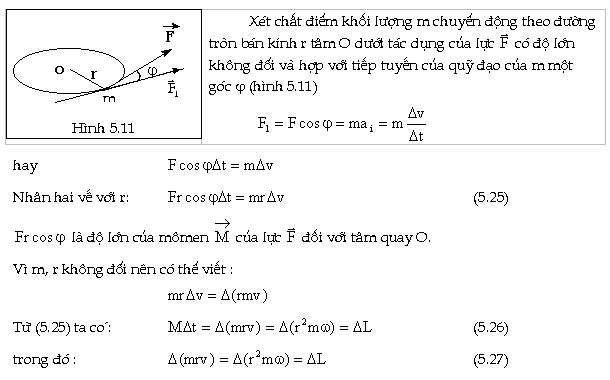
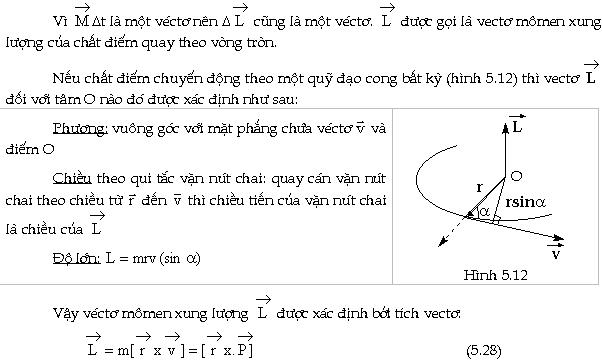

|
2. Mômen xung lượng của một
vật rắn quay quanh một trục
|

|
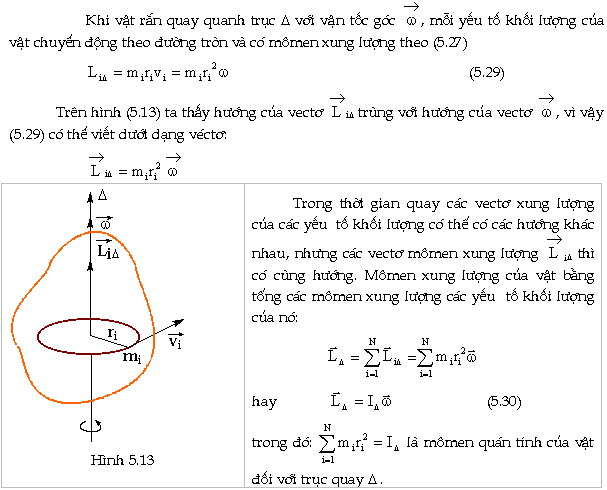
Vậy
Mômen xung lượng của vật rắn đối
với trục quay bằng tích mômen quán tính
của vật đối với trục đó
với vectơ vận tốc góc.
|
3. Ðịnh luật bảo toàn mômen xung lượng
|

|
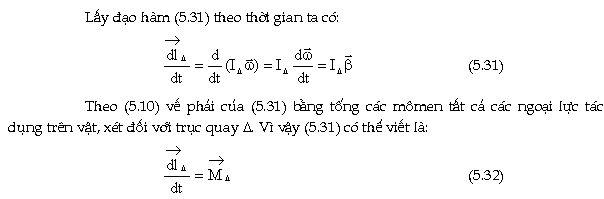
Phương
trình (5.32) biểu diễn định luật
biến thiên mômen xung lượng của vật
rắn. Cần chú ý rằng, phương trình
đó đúng cho bất kỳ hệ qui chiếu
nào, quán tính cũng như không quán tính, chỉ
cần chú ý rằng trong hệ qui chiếu không
quán tính, cần phải kể đến lực
quán tính đóng vai trò ngoại lực.
Từ
phương trình (5.32) ta đi tới kết
quả quan trọng sau đây:
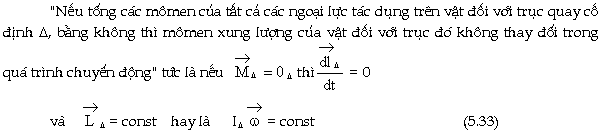
Biểu
thức trên là nội dung định luật
bảo toàn mômen xung lượng. Có thể suy
rộng định luật đó cho một
hệ vật quay quanh một điểm hay
một trục. Ðịnh luật bảo toàn mômen
xung lượng giống như các định
luật bảo toàn xung lượng và năng lượng,
là một trong những định luật cơ
bản của tự nhiên. Trong vật lý lí
thuyết, người ta đã chứng minh
rằng, định luật đó là kết
quả của tính đẳng hướng của
không gian.
TRỌNG
TÂM ÔN TẬP
***@@@***
1.
Biểu thức véctơ mômen lực đối
với một trục quay.
2.
Phương trình chuyển động quay cơ
bản.
3.
Biểu thức tính Mômen quán tính.
4.
Ðịnh lý Steiner về Mômen quán tính khi
chuyển trục quay.
5.
Năng lượng quay và tổng động
năng của vật rắn trong trường
hợp tổng quát.
6.
Mômen xung lượng và sự bảo toàn mômen
xung lượng.
BÀI
TẬP
***@@@***
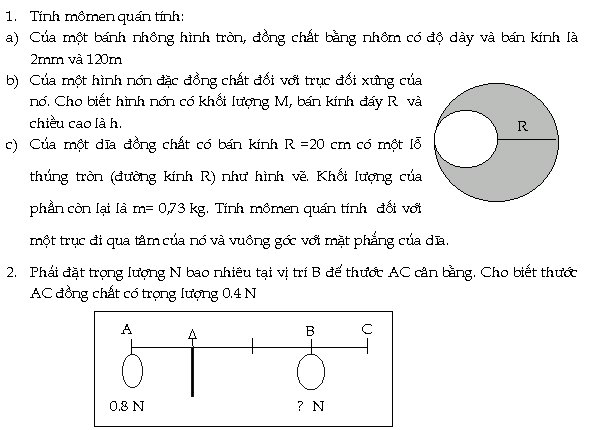
3.
Một quả cầu đặc đồng
chất khối lượng M, bán kính R .Lăn không
trượt từ trạng thái nghỉ trên đỉnh
một con dốc có chiều cao h. Tìm vận
tốc khối tâm của nó ở chân dốc.
- Từ
mức cao nhất của mặt phẳng
nghiêng, một hình cầu đặc và
một hình trụ đặc có cùng khối lượng
và bán kính bắt đầu lăn không trượt
xuống dưới. Tìm tỷ số của các
vận tốc của hai vật tại một
mức ngang nào đó.
- Trên
một hình trụ đặc và đồng
chất khối
lượng m và bán kính R ,người ta
quấn một sợi chỉ mảnh,
Một đầu sợi chỉ có
buộc khối lượng M. Lúc đầu
t=0 hệ bắt đầu chuyển động
quay quanh trục đi qua khối tâm. Bỏ qua
ma sát tại trục hình trụ
tìm sự phụ thuộc theo thời gian
của vận tốc góc của hình trụ . Tính
động năng toàn phần.
- Tính
động năng toàn phần của một
xe chuyển động với vận tốc V.
Bốn bánh xe là những hình trụ đặc
đồng nhất. Mỗi bánh có
khối lượng m. Khối lượng
của xe không kể bánh là M.
CÂU
HỎI TRẮC NGHIỆM
***&&&***

PHÂN
TÍCH NHỮNG CÂU PHÁT BIỂU ĐÚNG SAI
***@@@***
1.
Vật nào có mômen quán tính lớn thì sẽ
dễ dàng thay đổi vận tốc góc dưới
tác dụng mômen lực giống nhau.
2.
Với những trục quay khác nhau cùng đi
qua khối tâm, mômen của vật rắn sẽ có
cùng giá trị như nhau .
3.
Khi tác dụng một lực lên vật mà giá
của lực đó đi qua khối tâm thì
vật đó sẽ chuyển động tịnh
tiến.
4.
Khối tâm bao giờ cũng nằm bên trong
vật kể cả vật rỗng.
5.
Một xe chở đá và một xe chở
gổ có cùng khối lượng. Xe chở
gỗ cân bằng bền hơn.
6.
Thuyền sẽ bị chòng chành khi trên
thuyền có một người nào đó đứng
dậy.
7.
Hai dĩa tròn có cùng đường kính, dĩa
nào có khối lượng lớn thì mômen quán tính
của dĩa đó đối với trục
đi qua khối tâm sẽ lớn.
8.
Ðòn bẩy là một ứng dụng thực
tiển về tác dụng của mômen lực.


|