có
thể chia một cách tưởng tượng thành
một số các phần tử nhỏ tuỳ ý
so với kích thước của vật. Mỗi
phần tử nhỏ đó có thể coi là
một chất điểm. Do đó một
vật hay một hệ bất kỳ các vật có
thể coi như một hệ các chất điểm.
| I.
KHỐI TÂM VÀ CHUYỂN ÐỘNG CỦA
KHỐI TÂM.
|

|
Nếu
chia vật thành các phần tử nhỏ với
khối lượng nguyên tố mi thì có thể
biểu diễn vật như một hệ
chất điểm. Mỗi khối lượng
nguyên tố bất kỳ có thể chịu tác
dụng của các nội lực gây bởi
sự tương tác của nó với các
khối lượng nguyên tố khác trong vật
đang xét và các ngoại
lực. Chẳng hạn, nếu vật
nằm trong trọng trường của Trái Ðất
thì ngoại lực bằng mũ sẽ tác
dụng lên mỗi khối lượng nguyên
tố mi của vật.
Ðối
với khối lượng nguyên tố ta hãy
viết phương trình định luật 2
Newton:

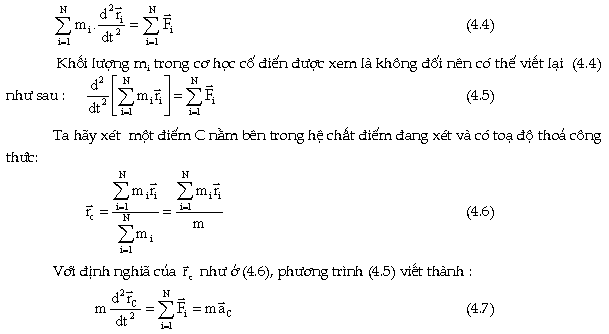
Ðiểm
C đó được gọi là khối tâm hay tâm
quán tính của hệ. Ở đây m là tổng
khối lượng của hệ vàĠ là gia
tốc của khối tâm. Có nghĩa là khối tâm
của một hệ vật chuyển động
như một chất điểm có khối lượng
bằng khối lượng của hệ vật
chuyển động dưới tác dụng
của tất cả các ngoại lực đặt
lên hệ
vật.
Trong
hệ toạ độ Descartes khối tâm của
vật được xác định bằng các
hình chiếu của chất điểm C lên các
trục toạ độ.
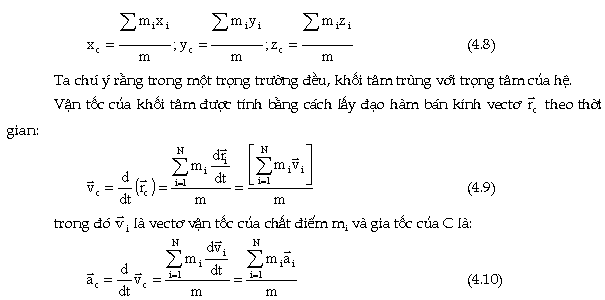
Phương
trình (4.7) cho phép thiết
lập sự chuyển động của khối
tâm của hệ vật nếu biết khối lượng
của hệ và các lực tác dụng lên nó.
| II.
XUNG LƯỢNG TOÀN PHẦN VÀ ÐỊNH
LUẬT BẢO TOÀN XUNG LƯỢNG.
|
|
|
1. Xung lượng toàn phần của hệ
|

|

|
2. Ðịnh luật bảo toàn xung lượng
|

|
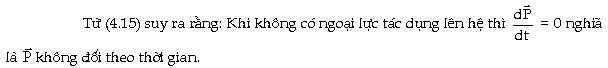
Ðiều
khẳng định này là nội dung của định
luật bảo toàn xung lượng được
phát biểu như sau: Xung lượng của
một hệ kín các chất điểm là không
đổi. Ngoài ra xung lượng của hệ cũng
không đổi ngay cả khi có lực ngoài tác
dụng với điều kiện tổng
cộng các ngoại lực tác dụng lên hệ
bằng không.
Trong
trường hợp khi tổng các ngoại
lực không bằng không nhưng hình chiếu
của tổng ngoại lực này lên một hướng
nào đó bằng không thì thành phần xung lượng
theo hướng đó
sẽ được bảo toàn.
Thật
vậy, chiếu (4.15) lên một phương x nào
đó, ta có:
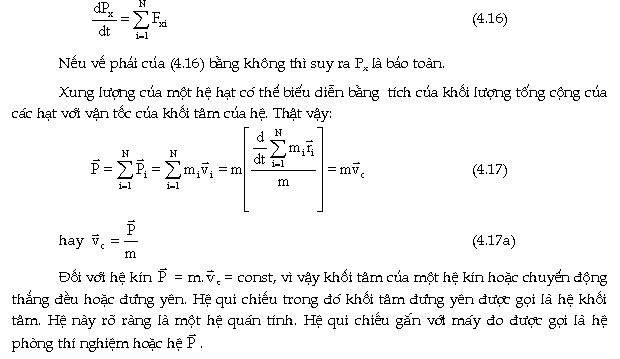
| III.
CƠ NĂNG TRONG HỆ
NHIỀU HẠT
|
|
|
1. Cơ năng của hệ
|

|
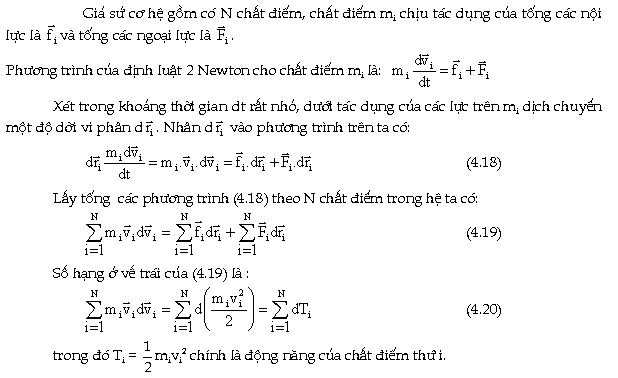
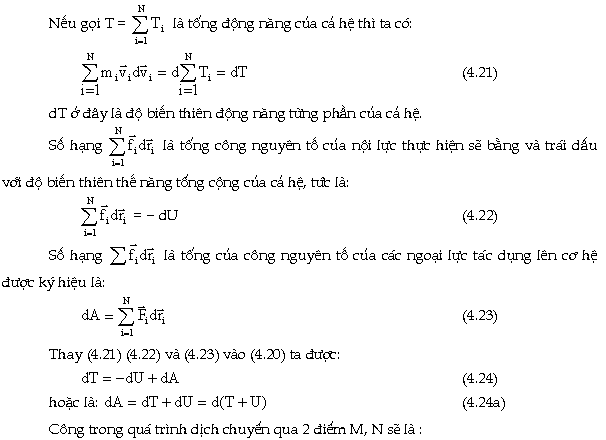

|
2.
định luật bảo toàn cơ năng
|

|
Trong
trường hợp hệ kín, không có ngoại
lực tác dụng vào hệ, phương trình
(4.25) trở thành.
E = T + U = const
(4.25b)
Như
vậy trong trường hợp hệ kín, các
nội lực đều là lực thế thì cơ
năng của hệ được bảo toàn.
Ðó chính là nội dung của định luật
bảo toàn cơ năng.
·Chú
ý là nếu trong các nội lực lại có
lực nội ma sát, ví dụ như chất điểm
mi chịu tổng các lực nội ma sátĠtác
dụng thì phương trình chuyển động
cho chất điểm mi sẽ khác đi và đóng
vai trò như các ngoại lực. Như thế cơ
năng của hệ không còn được
bảo toàn nữa. Tóm lại, trong hệ kín, có
tác dụng của các lực ma sát, cơ năng
của hệ giảm và chuyển hoá thành nội
năng của hệ.
Thông thường
ta hiểu va chạm là sự đụng độ
giữa các vật, mà hệ quả là sự
biến đổi đột ngột chuyển
động của chúng. Theo nghĩa rộng, va
chạm chỉ quá trình tương tác giữa các
vật. Thường ở những khoảng cách
lớn, tương tác không đáng kể; Khi các
vật lại gần nhau có
tương tác rất mạnh trong một
thời gian rất ngắn, có khi chỉ trong
một phần nghìn giây hay nhỏ hơn nữa.
Kết quả tương tác có thể rất khác
nhau tuỳ theo các điều kiện tương
tác xảy ra. Sau
va chạm hai vật tương tác có thể dính
lại làm một, có thể
tạo ra những vật mới hoặc có
thể là va chạm mà cơ năng của hệ
là không đổi.
|
2.
Các loại va chạm
|

|
Nếu phân biệt theo nội năng của
hệ ta có 2 loại va chạm là va chạm đàn
hồi và va chạm không đàn hồi.
Va chạm
đàn hồi là va chạm trong đó trạng thái
bên trong của các vật vẫn như cũ, cơ
năng của hệ không biến đổi. Trong
va chạm đó động năng chuyển
một phần hoặc hoàn toàn thành thế năng
biến dạng đàn hồi. Sau va chạm các
vật trở lại hình dạng ban đầu và
đẩy nhau. Vậy va chạm đàn hồi là
va chạm mà nội năng của hệ không
đổi dU=const và nó thường xảy ra trong
các hiện tượng nguyên tử. Một
số trường hợp va chạm thông thường
cũng có thể xem là đàn hồi.
Va
chạm có kèm theo sự biến đổi
trạng thái bên trong của vật, như vật
bị biến dạng, biến đổi
nhiệt độ... thì được gọi là
va chạm không đàn hồi. Trong va chạm không
đàn hồi có sự chuyển hóa của các
dạng cơ năng thành nhiệt năng hay
nội năng của hệ. Sau va chạm các
vật va chạm dính lại và chuyển động
với cùng một vận tốc.
Nói
chung mọi va chạm đều ít nhiều là không
đàn hồi: một phần động năng
của vật biến thành nhiệt làm vật nóng
lên, hoặc biến thành công làm vật biến
dạng.
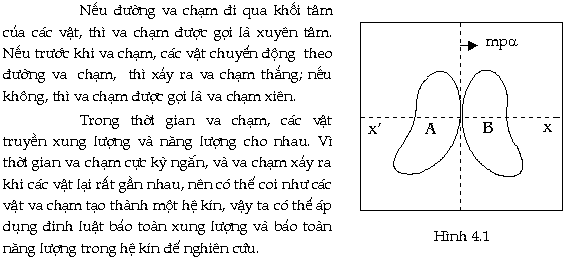
Người
ta cũng thường phân biệt va chạm xiên
và va chạm thẳng, va chạm xuyên tâm và không
xuyên tâm. Ta qui ước đường thẳng
đi qua điểm tiếp xúc của các vật
khi va chạm đồng thời vuông góc với
mặt phẳng va chạm gọi là đường
va chạm.
|
3.
Va chạm không đàn hồi
|

|

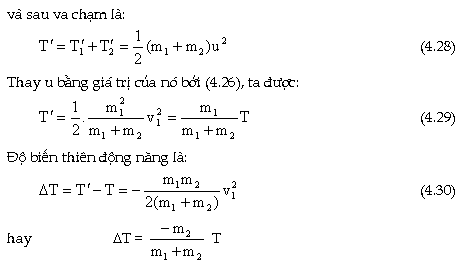
Kết
quả này dùng cho va chạm thẳng xuyên tâm không
đàn hồi tuyệt đối của hai
vật bất kỳ.
Theo
định luật bảo toàn năng lượng,
phần động năng này không biến
mất đi, mà được chuyển hoá thành
nội năng làm cho vật
nóng lên, hoặc biến thành công của nội
lực làm vật biến dạng. Do đó
nếu gọi U là
độ biến đổi nội năng khi
đó ta có:

|
4.
Va chạm đàn hồi
|

|
Như đã thấy trong va chạm không đàn
hồi, do các vật bị biến dạng,
hoặc biến đổi nhiệt độ sau
va chạm, nên cơ năng của hệ vật
không được bảo toàn.
Ngược lại, trong va chạm đàn
hồi, trạng thái của hệ vật
được bảo toàn. Vì trước và sau
va chạm, hai vật coi như không tương tác,
tức thế năng tương tác coi như không
có, nên sự bảo
toàn cơ năng chỉ còn là bảo toàn động
năng.

Như
vậy, nếu một vật nhỏ va chạm
với một vật lớn hơn nhiều, đang
đứng yên, thì vận tốc của vật
nhỏ sau va chạm chỉ đổi hướng
mà không đổi về độ lớn.

c)
Trường hợp 3 : Va chạm thẳng, xuyên tâm.
Lúc
này, các vận tốc có cùng phương.
Các phường trình (4.33) và (4.34) có thể
viết lại như sau: 
d)
Trường hợp tổng quát

Nghĩa
là, độ lớn xung lượng của
mỗi vật đều không thay đổi. Như
vậy, điều duy nhất xảy ra trong va
chạm là sự quay của vectơ xung lượng,
và do vectơ vận tốc của mỗi vật
cũng chỉ quay một góc như thế, còn
độ lớn vẫn giữ nguyên, vận
tốc của vật này luôn ngược
chiều với vận tốc vật kia.
Góc
quay của vận tốc không thể xác định
chỉ bằng hai định luật bảo toàn
năng lượng và xung lượng, mà còn
phụ thuộc tính chất cụ thể của
tương tác và vị trí tương đối
của hai vật trước va chạm.
TRỌNG
TÂM ÔN TẬP
***@@@***
1.
Khái niệm khối tâm.
2.
Phương trình chuyển động cơ
bản của hệ nhiều hạt.
3.
Sự bảo toàn tổng xung lượng
của hệ nhiều hạt.
4.
Sự bảo toàn cơ năng của hệ
nhiều hạt.
5.
Va chạm đàn hồi, va chạm không
đàn hồi, va chạm xuyên tâm và không xuyên tâm.
BÀI
TẬP
***@@@***
1.
Tính khối tâm của hệ gồm 3 dĩa
tròn (theo hình vẽ) có bán kính lần lượt
là 2cm, 2cm và 4cm. Biết độ dày và khối lượng
riêng của chúng bằng nhau và bằng 3kg/dm3
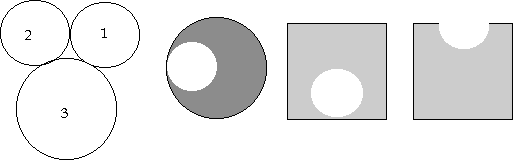
2.
Tính khối tâm của vật hình tròn có khoét
một hình tròn nhỏ phía trong có bán kính
bằng nửa hình tròn lớn và của hình vuông
cạnh là đường kính hình tròn lớn và
cũng khoét một hình tròn nhỏ phía trong (theo hình
vẽ).
3.
Một viên đạn khối lượng
m=10g bay với vận tốc 600 m/s.
Sau khi xuyên thủng một bức tường,
vận tốc chỉ còn 200 m/s. Tìm độ
biến thiên xung lượng và độ biến
thiên động lượng của viên
đạn. Tính lực cản trung bình mà
bức tường tác dụng vào viên đạn
cho biết thời gian mà viên đạn xuyên qua tường
là 1/1000 s.
4.
Sau va chạm đàn hồi của hai quả
cầu có khối lượng bằng nhau, cả
hai có cùng vận tốc sau là 10 m/s. Cho biết trước
va chạm quả cầu thứ hai đứng yên.
Tính góc tạo bởi phương chuyển động
của quả cầu thứ hai so với phương
chuyển động của quả cầu thứ
nhất trước khi va chạm. Tính vận
tốc của quả cầu thứ nhất trước
va chạm.
5.
Con lắc gồm một thanh mãnh khối lượng
không đáng kể ,chiều dài l=1,5m. Ở đầu
có đặt một quả cầu thép khối lượng
M=1 kg. Một quả cầu nhỏ cũng bằng
thép khối lượng m=20 g bay ngang đến
đập vào quả cầu M với vận
tốc v= 50 m/s. Coi va chạm là xuyên tâm đàn
hồi. Xác định góc lệch cực đại
của con lắc.
6.
Người ta dùng một búa máy có trọng
lượng p1= 900 N để đóng một
chiếc cọc có trọng lượng là p2 = 300
N vào đất. Mỗi lần đóng cọc lún
sâu được một khoảng h=5cm.
a)
Xác định lực cản của đất lên
cọc. Biết búa rơi từ độ cao H=2 m
xuống đầu cọc và lực cản
của không khí vào búa khi rơi là F= 0,07P1. Xem va
chạm giữa búa và cọc là tuyệt đối
không đàn hồi.
b)
Hãy tính phần năng lượng của búa
bị tiêu hao để làm nóng và biến
dạng trong va chạm giữa búa và cọc. Hãy tính
phần năng lượng dùng để
thắng lực cản của đất.
CÂU
HỎI TRẮC NGHIỆM
***@@@***
1.
Vật khối
lượng 30g chuyển động với
vận tốc V va chạm xuyên tâm với vật
khối lượng m thì
vận tốc của nó giảm một nửa.
Khối lượng m bằng:
a)
30 g b)
90 g
c)
60 g
d) 10 g
e)
20 g
2.
Một người đang chèo thuyền, dùng
cây chèo đẩy một khúc gỗ đang
chắn ngang dòng nước về phiá trước
do đó vận tốc của thuyền sẽ:
a)Tăng
lên.
b) Giảm xuống.
c) Không thay
đổi.
d)
Bằng không.
3.
Một người đang đứng yên trên
một con thuyền đứng yên. Nếu người
ấy đi từ mũi đến lái con
thuyền thì con thuyền sẽ:
a) Tiếp
tục đứng yên.
b)
Chuyển động cùng chiều với người.
c) Chuyển
động theo phương vuông góc với người.
d) Chuyển động ngược chiều
với người .
e)
Ngập sâu hơn trong nước.
4.
Va chạm giữa một quả bóng và khung
thành là va chạm:
a)
Ðàn hồi.
b) Xuyên tâm.
c) Không đàn hồi.
d) Không xuyên
tâm
e) Ðàn hồi và không xuyên tâm.
PHÂN
TÍCH NHỮNG CÂU PHÁT BIỂU ĐÚNG SAI
***%%%***
1.
Ðộng cơ phản lực hoạt động
trên cơ sở sự
bảo toàn xung lượng của hệ hai
vật.
2.
Một người nhảy từ
trên bờ xuống thuyền theo phường
ngang với vận tốc lớn thì người
và thuyền cùng đi xa bờ .
3.
Khi viên đạn bắn ra khỏi nòng súng,
cả súng và đạn đều chuyển động
về phía trước.
4.
Dùng một búa cao su để đóng đinh,
thì đầu đinh sẽ không bị biến
dạng.
5.
Khi chống xuồng trên
kinh rạch, không có ngoại lực tác
dụng lên hệ người và xuồng.
6.
Khi rèn dao phải đặt thanh sắt dưới
một chiếc đe thật nặng.
7.
Thổi căng một quả bóng bay, không
buột chặt miệng rồi buông tay ra, quả
bóng sẽ chuyển động.

 |