Lực Vạn Vật Hấp Dẫn

 

CÁC ÐỊNH LUẬT KEPLER    ÐỊNH LUẬT VẠN VẬT HẤP DẪN                  HẰNG SỐ HẤP DẪN- THÍ NGHIỆM CAVENDISH                TRƯỜNG HẤP DẪN-THẾ NĂNG TRƯỜNG HẤP DẪN     Trường hấp dẫn                                    Trường hấp dẫn tuân theo nguyên lý chồng chất           Công của lực hấp dẫn                                Thế năng của trường hấp dẫn                           Trọng Trường                              CÁC VẬN TỐC VŨ TRỤ

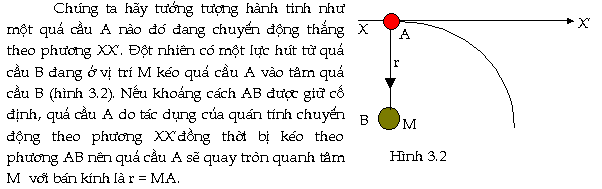
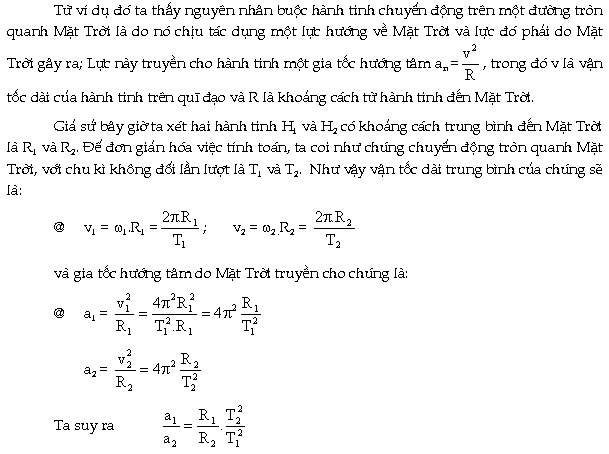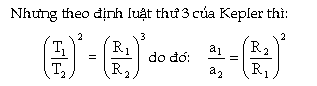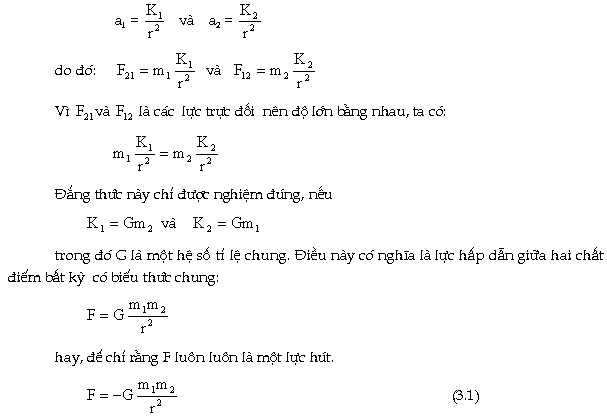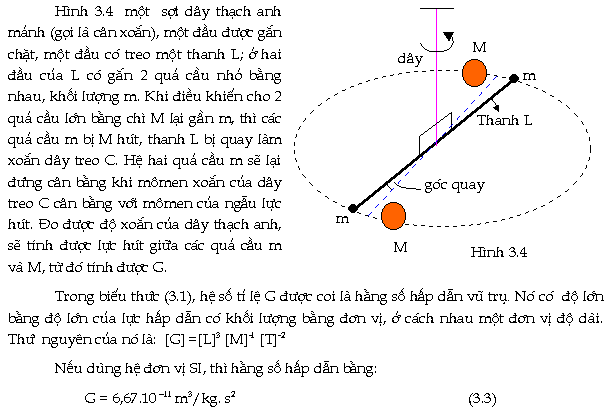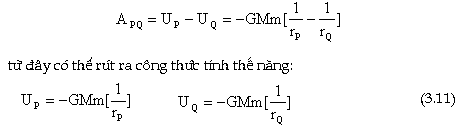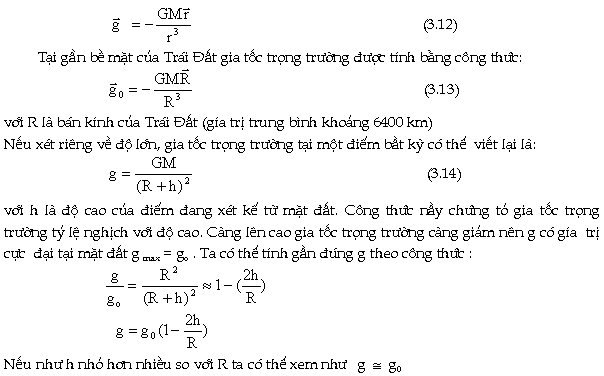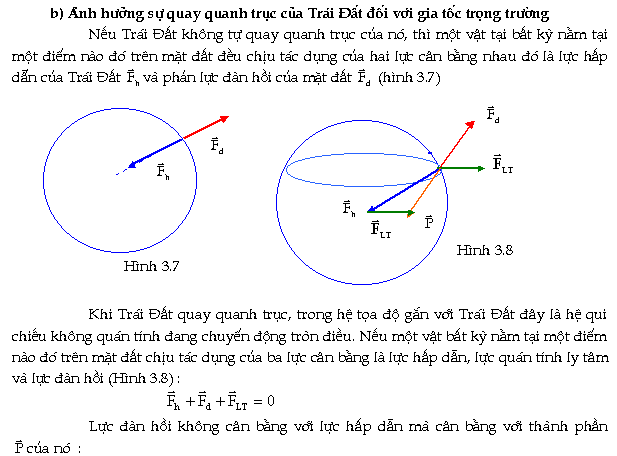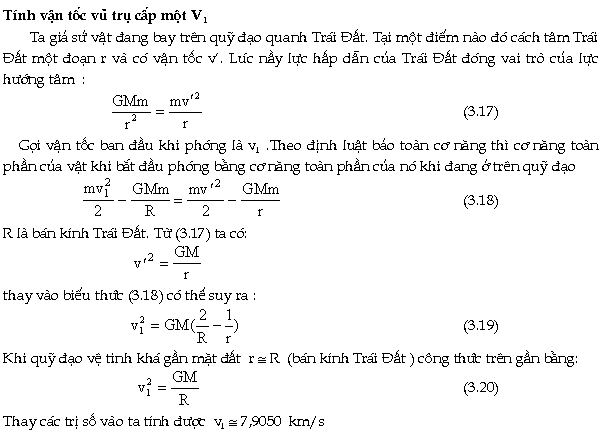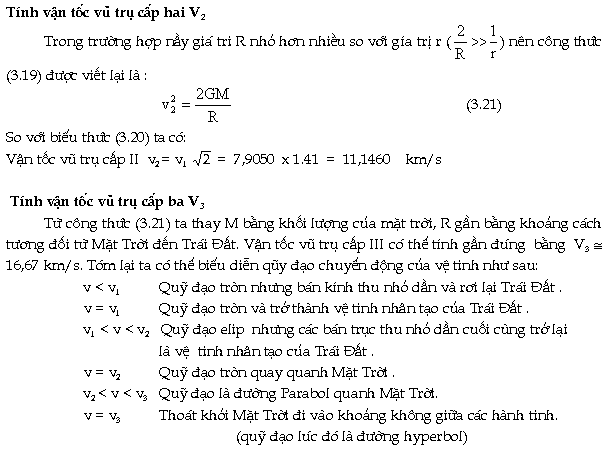I. CÁC ÐỊNH LUẬT KEPLER Sau khi đã tìm ra các định luật chuyển động, một vấn đề làm Newton suy nghĩ nhiều là: tại sao Mặt Trăng lại quay được quanh Trái Ðất, các hành tinh lại quay quanh Mặt Trời ? Kepler (1571 - 1630) đã tìm ra ba định luật chuyển động của các hành tinh, song không giải thích được nguyên nhân nào đã buộc các hành tinh chuyển động như vậy. Ba định luật kepler được phát biểu như sau: Ðịnh luật 1             Mọi hành tinh đều quay quanh Mặt Trời theo những quĩ đạo elip, mà Mặt Trời nằm ở một trong hai tiêu điểm. Suy nghĩ về nguyên nhân khiến các hành tinh phải chuyển động theo các định luật Kepler, kết hợp với các kết quả quan sát, Newton đã từng bước đi đến việc phát minh ra định luật vạn vật hấp dẫn. Từ ví dụ đó ta thấy nguyên nhân buộc hành tinh chuyển động trên một đường tròn quanh Mặt Trời là do nó chịu tác dụng một lực hướng về Mặt Trời và lực đó phải do Mặt Trời gây ra; Lực này truyền cho hành tinh một gia tốc hướng tâm an Ľ, trong đó v là vận tốc dài của hành tinh trên quĩ đạo và R là khoảng cách từ hành tinh đến Mặt Trời.                                    Nghĩa là gia tốc do mặt trời truyền cho hành tinh tỉ lệ nghịch với bình phương khoảng cách từ hành tinh đến Mặt Trời. Sở dĩ các hành tinh quay quanh Mặt Trời, là vì chúng chịu tác dụng của một lực xuất phát từ  Mặt Trời; vậy lực buộc Mặt Trăng quay quanh Trái Ðất cũng phải là một lực xuất phát từ Trái Ðất. Nếu như Trái Ðất có nhiều Mặt Trăng, thì gia tốc hướng tâm do Trái Ðất truyền cho mỗi Mặt Trăng sẽ tỉ lệ nghịch với bình phương khoảng cách từ Mặt Trăng đó đến tâm Trái Ðất. Và nếu như có Mặt Trăng nhỏ bay là là trên Mặt Ðất, thì gia tốc hướng tâm của nó sẽ lớn hơn gia tốc hướng tâm của Mặt Trăng thực khoảng 602 lần (vì khoảng cách từ Mặt Trăng thực đến tâm Trái Ðất bằng khoảng 60R, với R ( 6400 Km là bán kính của Trái Ðất) tức là xấp xỉ bằng gia tốc rơi tự do trên Trái Ðất. Suy nghĩ như vậy, Newton quyết định kiểm tra lại vấn đề này. Theo các số liệu quan sát thiên văn thời bấy giờ, khoảng cách từ Mặt Trăng đến tâm Trái Ðất bằng khoảng d=60R, tức là xấp xỉ 3,84.108m, chu kỳ quay của nó quanh Trái Ðất khoảng 27 ngày 7 giờ  43 phút, từ đó Newton tính ra gia tốc hướng tâm của Mặt Trăng là: Vậy lực tác dụng của Mặt Trời lên các hành tinh, của Trái Ðất lên Mặt Trăng là cùng bản chất với lực do Trái Ðất tác dụng lên mọi vật trên mặt đất (trọng lực), nghĩa là cùng bản chất là lực hấp dẫn. Do đó, mọi lực hấp dẫn, cũng như lực hấp dẫn của Mặt Trời lên các hành tinh, đều do chung một đặc điểm là tỉ lệ nghịch với bình phương khoảng cách. Suy rộng hơn nữa, Newton đi đến kết luận là lực hâïp dẫn không chỉ tác dụng giữa các thiên thể, mà là một lực phổ biến, tác dụng giữa mọi vật bất kỳ với nhau.  II.  ÐỊNH LUẬT VẠN VẬT HẤP DẪN Giả sử có 2 chất điểm có khối lương m1­ và m2, đặt cách nhau một khoảng r Theo tính toán đã trình bày ở mục trên, các gia tốc này đều tỉ lệ nghịch với bình phương khoảng cách giữa chúng r , nghĩa là: Nghĩa là hai phần tử vật chất bất kì bao gờ cũng hút nhau với một lực tỉ lệ thuận với với hai khối lượng, tỉ lệ nghịch với bình phương khoảng cách giữa chúng. Với các vật có kích thước đáng kể so với khoảng cách giữa chúng, phải chia chúng thành từng phần nhỏ, tính lực hấp dẫn của từng cặp bằng công thức (3.1), rồi lấy tổng của các lực này. Riêng trường hợp vật hình cầu, có khối lượng phân bố đối xứng qua tâm, thì vẫn có thể áp dụng ngay công thức (3.1) để tính lực hấp dẫn, vì lúc này có thể coi như khối lượng của mỗi vật tập trung ở tâm. Viết dưới dạng vectơ, biểu thức (3.1) có dạng: III. HẰNG SỐ HẤP DẪN- THÍ NGHIỆM CAVENDISH Cavendish là người đầu tiên đã đo được trị số của G bằng thực nghiệm, vào năm 1797. Thí nghiệm khá tỉ mỉ,  song về nguyen tắc có thể trình bày tóm tắc như sau Nếu như có được một lực kế rất nhạy, đo được lực hấp dẫn giữa hai vật thông thường nào đó, thì  từ đó có thể tính được trị số của G IV. TRƯỜNG HẤP DẪN - CƯỜNG ÐỘ TRƯỜNG HẤP DẪN           1. Trường hấp dẫn Biểu thức của lực hấp dẫn không có chứa số hạng thời gian nghĩa là lực hấp dẫn có thể truyền tức thời trong  không gian. Khoa học  ngày  nay không thừa nhận quan điểm truyền tương tác đi tức thời, hay còn gọi là quan điểm tương tác xa. Mọi tương tác đều truyền đi với vận tốc giới hạn, không vượt quá vận tốc ánh sáng là 300 000 km/s. Ðó là quan điểm tương tác gần. Ðối với tương tác hấp dẫn ta có thể hiểu quan điểm nầy như sau : Khối lượng m1 tự nó đã tạo ra trong không gian xung quanh một trường lực được gọi là  trường hấp dẫn, tức là m1 xuất hiện đã làm thay đổi tính chất vật lý của không gian xung quanh và nếu đặt một chất điểm m2 khác vào trong trường đó thì m2 lập tức bị môt lực  lực kéo về phía m1 . Lực nầy có độ lớn xác định bởi biểu thức:           2.Trường hấp dẫn tuân theo nguyên lý chồng chất           3. 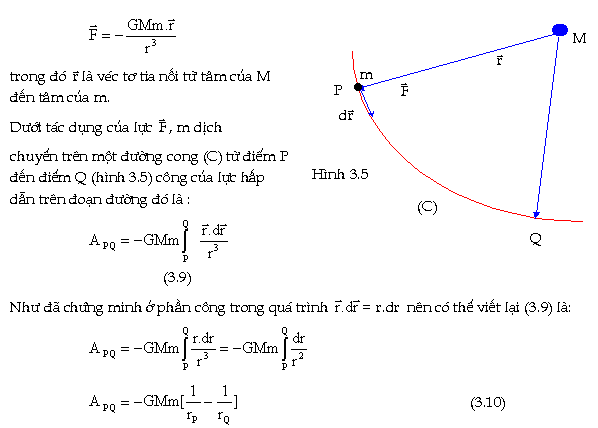Công của lực hấp dẫn            Xét một chất điểm m bất kỳ nằm trong trường hấp dẫn tạo ra bởi một khối lượng M. Khối lượng m chịu tác dụng một lực hấp dẫn:      Công thức nầy chứng tỏ rằng  công của lực hấp dẫn không phụ thuộc dạng đường đi mà phụ thuộc vị trí đầu và vị trí cuối. Ðiều nầy chứng tỏ trường hấp dẫn là một trường thế.           4. Thế năng của trường hấp dẫn  Dựa vào biểu thức liên hệ giữa thế năng và trường hấp dẫn (chương 2) ta có:  Các điểm trong trường hấp dẫn có cùng một giá trị thế năng tạo thành một mặt gọi là mặt đẳng thế. Một chất điểm nếu dịch chuyển trên một mặt đẳng thế thì không sinh công bởi vì thế năng điểm đầu và thế năng điểm cuối là như nhau. Như vậy, lực tác dụng phải có phương vuông góc với phương dịch chuyển.             5.Trọng trường Trường hấp dẫn của Trái Ðất, do khối lượng của Trái Ðất tạo ra ở  gần bề mặt của nó được gọi là trọng trường. Chính trọng trường là nguyên nhân làm cho mọi vật phải rơi vào bề mặt của Trái Ðất, giữ cho trái đất có một lớp khí quyển bao quanh. Lớp khí nầy bảo vệ mọi sinh vật trên Trái Ðất và Trái Ðất tránh được tác hại từ các bức xạ mạnh phát ra từ trong vũ trụ.            Véctơ cường độ trường hấp dẫn của Trái Ðất còn được gọi là gia tốc trọng trường và được xác định bởi công thức Trong trường hợp h lớn hơn rất nhiều so với R,  g sẽ tiến đến không, lực hấp dẫn tại đó có thể xem bằng không.     V. CÁC VẬN TỐC VŨ TRỤ   Ðịnh luật vạn vật hấp dẫn được dùng để tính các vận tốc tối thiểu để phóng một vật từ mặt đất chuyển động trên những quỹ đạo khác nhau .             Nếu vật chuyển động theo quỹ đạo tròn quanh Trái Ðất thì vật đó trở thành vệ tinh nhân tạo của trái đất và vận tốc v1 cần thiết tối thiểu phải truyền cho vật để đạt được quỹ đạo đó gọi là vận tốc vũ trụ cấp I (hình 3.9a). Ðể cho vật có thể vượt ra khỏi sức hút của trái đất và chuyển động theo qũy đạo Elip quanh mặt trời trờ thành  hành tinh nhân tạo của Mặt Trời thì  vận tốc cần thiết tối thiểu v2  khi phóng phải lớn hơn vận tốc vũ trụ cấp I và được gọi là vận tốc vũ trụ cấp II  (hình 3.9b). Khi tăng vận tốc phóng cao hơn vận tốc vũ trụ cấp II, bán kính của quỹ đạo elip của vật quanh Mặt Trời tăng dần, Khi vận tốc nầy đạt đến một gía trị Vmax  xác định thì vật sẽ thoát khỏi Mặt Trời và đi vào vũ trụ . Vận tốc V max được gọi là vận tốc vũ trụ cấp III(v3 )(hình 3.9c).        TRỌNG TÂM ÔN TẬP ***&&&*** Các định luật Kepler. Ðịnh luật hấp dẫn -Hằng số hấp dẫn. Cường độ trường hấp dẫn -Véc tơ cường độ trường hấp dẫn. Nguyên lý chồng chất trường hấp dẫn. Thế năng của trường hấp dẫn. Trọng trường, gia tốc trọng trường. Các vận tốc vũ trụ .   BÀI TẬP ***@@@*** 1.      Sao Hỏa có bán kính trung bình là 3400 km. Sao Hỏa có hai vệ tinh quay xung quanh là Deimos và Phobos. Khoảng cách trung bình từ Deimos đến Sao Hỏa là 23500 km. Thời gian Deimos quay một vòng quanh quỹ đạo là T= 30,3 giờ . Tính khối lượng Sao Hỏa, khối lượng riêng trung bình của Sao Hỏa và gia tốc hấp dẫn trên bề mặt Sao Hỏa. 2.      Hai khối lượng M và 3M đặt cách nhau một đoạn là h. Phải đăt một khối lượng m vào nơi nào để cho tổng lực hấp dẫn của M và 3M đặt lên vật m bị triệt tiêu. 3.      Tính vận tốc vũ trụ cấp một và cấp hai đối với Mặt Trăng. So sánh kết quả khi tính ở Trái Ðất. 4.      Ở độ cao nào trên cực bắc của Trái Ðất, gia tốc trọng trường giảm 1/100 và giảm 1/2 lần. 5.      Tính năng lượng tối thiểu để đưa một con tàu vũ trụ có khối lượng là 2 tấn từ Trái Đất Lên Mặt Trăng 6.      Tính khoảng cách đối với mặt đất của một vệ tinh địa tĩnh .Cho biết bán kính và khối lượng Trái Ðất là R=6370 km, M= 5,974. 10 24 kg. Chu kỳ quay của trái đất quanh trục là T= 24 giờ .   CÂU HỎI TRẮC NGHIỆM ***&&&*** Nơi có gia tốc trọng trường lớn nhất tính theo vĩ độ địa lý là: a) Huế           b) Cao bằng        c) Cần Thơ        d) Cà mau         e) TP. Hồ Chí Minh   Hãy chọn một nơi mà gia tốc trọng trường của có giá trị nhỏ nhất : a)  Tâm Trái Ðất          b) Tại xích đạo                       c) Cực bắc     d) Ðộ cao 1 km so với mặt đất                                   e) Tại tâm Mặt Trăng   Bán kính Trái Ðất gấp 1,88 lần bán kính Sao Hỏa. Khối lượng Trái Ðất gấp 9,09 lần khối lượng Sao Hỏa. Tỉ số gia tốc trên bề mặt đất so với gia tốc trên bề mặt Sao Hỏa: a)      0,39                              b) 0,2              c) 43,8                    d)  2,56               e)   4,8   Ở độ cao nào trên địa cực gia tốc giảm một nửa :             a) 32 km          b) 32 m        c)1600 km       d) 1,6 km        e)  Một gía trị nào đó.   PHÂN TÍCH NHỮNG CÂU PHÁT BIỂU ĐÚNG SAI ***%%%*** 1.     Càng đi vào tâm Trái Ðất gia tốc trọng trường càng giảm. 2.     Mọi vật khi ném lên đều phải rơi lại Trái Ðất. 3.     Người ta có thể cân đúng một vật bằng một chiếc cân sai và những quả cân đúng. 4.     Hai chiếc tàu có trong tải trên 10 tấn, chạy  gần nhau sẽ hút nhau rất mạnh. 5.     Một số nơi trên Trái Ðất, trọng lượng bằng trọng lực.