|
Chương
trước chúng ta đă đi qua các kiểu
dữ liệu đơn giản là các dữ
liệu kiểu dữ liệu vô hướng
chuẩn (Standard Scalar-type Data) như Integer, Real,
Char, Boolean. Các kiểu này đă được
định nghĩa sẵn trong mọi chương
tŕnh cài đặt trong máy. Ngôn ngữ Pascal cho phép
người lập tŕnh có thể tự đặt
ra các kiểu vô hướng mới bằng cách
tự liệt kê các giá trị của kiểu vô
hướng mới và phải khai báo định
nghĩa kiểu. Danh sách các giá trị này
được đặt trong ngoặc đơn
( ) và được mô tả bằng một tên
kiểu (như phần mô tả kiểu TYPE).
Kiểu vô hướng theo cách này gọi là
kiểu vô hướng liệt kê (Enumerated Scalar
Type). Có
2 cách khai báo một biến kiểu liệt kê: + Khai báo gián tiếp: Định nghĩa kiểu (dựa vào từ khóa type) trước khi khai biến (var)
TYPE
<tên kiểu liệt kê> = (<danh sách giá
trị kiểu liệt kê>) ;
VAR
<danh sách biến> : <tên kiểu
liệt kê> ; Ví
dụ 8.1:
TYPE
Days = (Sun,
Mon, Tue, Wed, Thu, Fri, Sat) ;
Colors =(Red, Yellow, Green, White, Blue, Black) ;
Subjects = (Mathematics, Physics, Chemistry, Biology) ;
VAR
Ngay : Days ;
MauVe : Colors ;
MonThi, Kiemtra :
Subjects ;
+ Khai báo trực tiếp: Kiểu sau biến được định nghĩa trực tiếp.
VAR <danh sách biến> : (<danh sách giá trị kiểu liệt kê>) ; Ví
dụ 8.2:
VAR
Ngay : (Sun, Mon, Tue, Wed, Thu, Fri, Sat) ;
MauVe : (Red, Yellow, Green, White) ; Ta
có thể gán cho biến các giá trị của
kiểu tương ứng:
Ngay := Mon ;
MauVe := Red ; Biến
theo định nghĩa của kiểu nào chỉ
nhận giá trị của kiểu đó mà thôi. Theo
khai báo như ví dụ 8.2. ở
trên, ta không thể có
MauVe := Mon ; Kiểu
vô hướng liệt kê là một kiểu đếm
được. Theo
định nghĩa kiểu vô hướng
liệt kê, thứ tự danh sách giá trị
liệt kê được ngầm đánh số tăng
tuyến tính bắt đầu từ số 0
trở đi theo thứ tự từ trái sang
phải. Như vậy, ở ví dụ trên: Sun <
Mon < Tue < Wed .... và
Red < Yellow < Green ... *
Hàm thứ tự ORD (X) Hàm
này cho ta thứ tự của giá trị x trong
kiểu vô hướng đếm được.
Hàm ORD thực chất là hàm biến đổi
một giá trị kiểu vô hướng đếm
được sang giá trị kiểu số nguyên. Theo
ví dụ trên:
ORD (Sun) = 0
là Đúng v́ Sun có thứ tự là 0
ORD (Mon) = 1
là Đúng v́ Mon có thứ tự là 1
ORD (Green) = 3
là Sai v́ Green có thứ tự là 2
ORD (n) = n
trong đó n là một giá trị kiểu
Longint *
Hàm PRED (X) Hàm
này cho giá trị đứng trước x trong
định nghĩa kiểu của x. Theo
ví dụ trên :
PRED (Mon) = Sun
PRED (Green) = Yellow
PRED (n) = n - 1 *
Hàm SUCC (X) Hàm
này cho giá trị đứng sau x trong định
nghĩa kiểu của x. Theo
ví dụ trên:
SUCC (Mon) = Tue
SUCC (Green) = White
SUCC (n) = n + 1 *
Hàm chuyển một số nguyên thành một giá
trị vô hướng Tên
hàm này chính là tên kiểu vô hướng mà ta
đă khai báo trước. Theo
ví dụ trên:
Days(2) = Tue
Colors(3) = White
LONGINT (n) = n Viết
và đọc theo kiểu liệt kê th́ khác
với kiểu vô hướng chuẩn. *
Viết ra kiểu liệt kê Thủ
tục Write và Writeln chỉ chấp nhận
đưa ra các giá trị thuộc kiệu vô hướng
chuẩn (Real, Integer, Byte, Char, Boolean) mà không
chấp nhận viết ra một giá trị
kiểu vô hướng liệt kê, ví dụ cách
viết sau là không đúng:
Writeln(Color(4))
Writeln(Red)
Writeln(Days) mà
chỉ có thể chấp nhận nếu viết:
Writeln (Char(78))
v́ Char(78) = N là giá trị vô hướng
chuẩn. Để
viết ra một giá trị của biến vô hướng
liệt kê, ta có thể áp dụng thủ
thuật sau:
IF MauVe = Red THEN
Writeln(‘Red’) ;
*
Đọc vào kiểu liệt kê Thủ
tục Read và Readln cũng chỉ chấp nhận
đọc vào một giá trị kiểu vô hướng
chuẩn mà không chấp nhận đọc
trực tiếp các giá trị kiểu vô hướng
liệt kê, ví dụ không thể đọc
Readln(Days). Để đọc vào một giá trị
kiểu liệt kê ta có thể dùng phương pháp
sau: đọc số thứ tự của giá
trị biến vô hướng rồi biến
đổi kiểu dữ liệu thêm: Ví
dụ 8.3:
TYPE Days
= (Sun, Mon, Tue, Wed, Thu, Fri, Sat) ;
VAR i
: Integer ;
BEGIN
Write('Nhập số từ
0 . .6 tương ứng cho ngày:'); Readln(i) ;
Case Days(i) of
Sun: writeln('Ngày Chủ nhật');
Mon: writeln('Ngày thứ hai');
Tue: writeln('Ngày thứ ba');
Wed: writeln('Ngày thứ tư');
Thu: writeln('Ngày thứ
năm');
Fri: writeln('Ngày thứ sáu');
Sat: writeln('Ngày thứ bảy');
Else writeln('Nhập sai');
end;
Readln;
END. Mục
2 ở phần II ở phía sau, sẽ giới
thiệu chuỗi String, ta có thể dùng thủ
thuật sau để đọc kiểu liệt kê: Ví
dụ 8.4:
Readln(St) ;
IF St = ‘Mon’ THEN Ngay := Mon ; a.
Khái niệm Khi
khai báo một số trường hợp, ví
dụ Tuổi của người hoặc Điểm
thi học sinh, nếu ta viết:
VAR
TuoiTho : Integer ;
{Integer có miền xác định -32 768 .. 32
767} Hay
Diem : Real ;
{Real có miền xác định 2.9 E-39 .. 1.7
E38} Nếu
viết như vậy sẽ tốn ô nhớ v́
Integer có kích thước 2 bytes hoặc Real có kích
thước đến 6 bytes. Làm như vậy
sẽ không cần thiết v́ Tuổi con người
chỉ biến thiên trong khoảng từ 0 đến
200 là lớn nhất và điểm thi học sinh
th́ chỉ trong khoảng từ 0 đến 10
chẳng hạn.
Trong Pascal cho phép ta xác định một
biến lấy giá trị trong một khoảng nào
đó được giới hạn ở một
hằng cận dưới (first data item) và một
hằng cận trên (last data item).
Hai giá trị này phải cùng một kiểu
vô hướng đếm được và
hằng cận trên có giá trị lớn hơn
hằng cận dưới. Khai báo như vậy
gọi là khai báo kiểu miền con (Sub-range type) và
biến của nó chỉ chiếm 1 byte trong ô
nhớ mà thôi. Trong lúc chạy chương tŕnh,
ta có thể kiểm tra giá trị của biến
không được vượt ra khỏi giới
hạn của khoảng con. Miền
con là một tập hợp con của một
kiểu đếm được. Có 2 cách khai báo: + Khai báo gián tiếp:
TYPE
<Tên kiểu miền con> = <hằng
cận dưới> .. <hằng cận trên>
;
VAR
<danh sách biến> : < Tên kiểu
miền con> ; Ví
dụ 8.5:
TYPE
TuoiTho = 0 .. 200 ;
VAR Tho
: TuoiTho ; + Khai báo trực tiếp:
VAR
<danh sách biến> : <hằng cận dưới>
.. <hằng cận trên> ; Ví
dụ 8.6:
VAR Tuoi
: 0 .. 200 ; Pascal
có 4 kiểu cấu trúc dữ liệu là kiểu
mảng (ARRAY), tập hợp (SET), bản ghi
(RECORD) và tập tin (FILE). Sau đây ta lần lượt
t́m hiểu từng kiểu cấu trúc. Một
mảng dữ liệu là một tập hợp
số hữu hạn phần tử có giống như
các biến, có cùng kiểu, gọi là kiểu cơ
bản.
Mảng được được tổ
chức theo một trật tự xác định.
Số phần tử của mảng được
khai báo ngay từ khi định nghĩa ra
mảng. Mảng
một chiều có thể được hiểu
như một danh sách các phần tử (theo
cột), có cùng kiểu. Mỗi phần tử
của mảng được xác định
được truy nhập trực tiếp thông
qua tên mảng cùng với chỉ dẫn truy
nhập được để giữa hai
ngoặc vuông [ ]. Ví
dụ 8.7:
List là một mảng 1 chiều có n phần
tử. Các phần tử của List có thể mang
các tên List[1], List[2], List[3], ..., List[n], và có thể
minh họa như h́nh sau:
List[1] List[2]
List[3] List[4]
.........
List[n]
H́nh 8.1: Minh họa mảng một chiều + Khai báo gián tiếp: TYPE
<Kiểu
mảng> = ARRAY
[Kiểu chỉ số ]
OF <Kiểu phần tử > ;
VAR
<Danh sách
biến> : Kiểu mảng ; + Khai báo trực tiếp :
VAR
< Danh sách biến > : ARRAY [ Kiểu
chỉ số] OF < Kiểu phần tử > ; *
Chú ư: Kiểu
chỉ số phải là kiểu rời rạc (đếm
được). Ví
dụ 8.8:
TYPE
KM1 = ARRAY [1.. 100] OF
INTEGER ;
KM2 = ARRAY [1 .. 20 ] OF CHAR ;
DAY = (Sun, Mon, Tue, Wed, Thu, Fri, Sat) ;
VAR
TUOI : KM1 ;
TEN : KM2 ;
NGAY : ARRAY [DAY] OF BOOLEAN ; Ư
nghĩa: -
KM1 là kiểu mảng gồm 100 phần
tử được
đánh số từ 1 đến 100 thông qua
kiểu chỉ dẫn là một miền con các
số nguyên từ 1 .. 100.
TUOI là biến có kiểu là KM1. -
KM2 là kiểu mảng gồm 20 phần
tử đánh số từ 1 .. 20 có kiểu là các
kư tự. Biến TEN có kiểu là KM2. -
NGAY là một biến mảng gồm 7
phần tử kiểu Boolean được đánh
dấu qua kiểu chỉ dẫn là tên của 7 ngày
trong tuần. Chú
ư: Khi
khai báo mảng, kiểu chỉ dẫn chỉ có
thể là: -
Kiểu miển con của các loại dữ
liệu vô hướng đếm được
như kư tự, số nguyên -
Kiểu liệt kê do người viết định
nghĩa (như NGAY trong tuần) -
Kiểu Boolean
Kiểu chỉ dẫn không thể là
kiểu không đếm được như REAL
Viết như sau là SAI :
X1 : ARRAY [Real] OF Integer ; Ta
cũng không thể khai báo như: X2 : ARRAY [Integer]
OF Integer ; Mặc
dầu Integer là kiểu vô hướng đếm
được do giới hạn của vùng
nhớ dành cho dữ liệu, số lượng
phần tử của 1 mảng cũng bị
hạn chế tùy theo kích thước của
kiểu dữ liệu của các phần tử,
ta nên dùng kiểu miền con để khai báo
số phần tử của mảng. +
Truy xuất các phần tử của mảng: Mỗi
phần tử của mảng được truy
xuất thông qua Tên Biến Mảng cùng với
chỉ số của mảng trong dấu ngoặc
vuông [ ]. Ví dụ tên biến mảng là A, khi
viết A[7], ta hiểu nó là phần tử thứ
7 của mảng A. Ví
dụ 8.9:
Lập tŕnh giải một bài toán tính trung
b́nh một dăy số x[i] :
x[1], x[2], x[3], ... , x[n] sau
đó tiếp tục tính độ lệch
(deviation) của từng phần tử so với
trị trung b́nh, theo công thức: độ_lệch
= x[i] - trung_b́nh
Giả sử dăy số của chúng ta có
giới hạn n = 100 phần tử trở
lại, n là một biến số để khai báo
số phần tử muốn tính PROGRAM
Average_deviations ;
{ Nhập n số phần tử kiểu
số thực, tính trị trung b́nh của chúng,
sau đó tính tiếp độ lệch
của từng phần tử số so với
trị trung b́nh } VAR
n, count : integer ;
sum, average, deviation : real ;
x : ARRAY [1 .. 100] OF real ; BEGIN
(* Nhập số phần tử và tính trung b́nh*)
Write (' Nhập bao nhiêu số n để tính
trung b́nh ? ') ;
Readln (n) ;
Writeln ;
sum := 0 ;
FOR count := 1 TO n DO
BEGIN
Write ( ‘ i = ‘, count : 3, ‘
x =
‘ ) ;
Readln (x [count] ) ;
sum := sum + x[count];
END ;
average := sum/n ;
Writeln (' Trung b́nh của dăy số là
= , average ') ;
Writeln ; (*
Tính độ lệch so với trị trung b́nh *)
FOR count := 1 TO n DO
BEGIN
deviation := x[count] - average ;
Write ( ‘ i = ‘, count : 3, ‘
x = ‘,
x[count] ) ;
Writeln (' Độ
lệch d = ,
deviation ');
END ;
Readln; END. Giả
sử, ta nhập vào 5 số hạng (các số có
gạch dưới là phần của người
nhập): x[1]
= 3.0
x[2] = -2.0
x[3] = 12.0
x[4] = 4.4
x[5] = 3.5 Khi
chạy chương tŕnh (nhấn Ctrl + F9), trên màn
h́nh ta sẽ thấy : Nhập
bao nhiêu số n để tính trung b́nh ? 5 i
=
1
x = 3.0 i
=
2
x = -2.0 i
=
3
x = 12.0 i
=
4
x = 4.4 i
=
5
x = 3.5 Trung
b́nh của dăy số là =
4. 1800000E+00 i
=
1
x = 3.
0000000E+00 Độ
lệch d = - 1. 1800000E+00 i
=
2
x = -2. 0000000E+00 Độ
lệch d = - 6. 1800000E+00 i
=
3
x = 1.
2000000E+00 Độ
lệch d = 7.
8200000E+00 i
=
4
x = 4.
4000000E+00 Độ
lệch d = 2.
2000000E - 01 i
=
5
x = 3.
5000000E+00 Độ
lệch d = - 6. 8000000E - 01 Ta
có thể định khoảng chừa kết
quả và phần lẻ thập phân, dùng lệnh
: m : n Ví
dụ 8.10:
Sắp xếp một dăy số theo thứ
tự từ nhỏ đến lớn Tiến
tŕnh của bài toán: -
Giả
sử chuỗi số của ta có n phần tử
-
Một
thủ tục (Procedure) sẽ làm công việc
sắp xếp như sau : đầu tiên đưa
phần tử thứ nhất so sánh với các
phần tử tiếp theo, nếu nó lớn hơn
phần tử so sánh th́ đem đổi chổ
giá trị của hai phần tử với nhau. Sau
đó tiếp tục đem phần tử thứ
2 so sánh các phần tử tiếp theo theo tŕnh
tự như vậy, ... và cứ như thế cho
đến phần tử thứ n - 1. -
In
kết quả ra màn h́nh Chương
tŕnh Pascal như sau: PROGRAM
Reorder ;
(* Sắp xếp một mảng các phần
tử số thực từ nhỏ đến
lớn*) VAR
n, i, loc: 1 .. 100 ;
x : ARRAY [1 .. 100] OF real ;
temp : real ; PROCEDURE
interchange ;
(* Đổi chỗ các phần tử mảng
từ nhỏ đến lớn*) BEGIN
FOR loc := 1 TO n-1 DO
FOR i := loc + 1 TO n DO
IF x[i] < x [loc] THEN
BEGIN
temp := x[loc] ;
x[loc] := x[i] ;
x[i] := temp ;
END ; END
; BEGIN
Write (' Có bao nhiêu phần tử số ?
') ; Readln
(n) ;
FOR i := 1 TO n DO
BEGIN
Write ( ‘ x[ ‘, i : 3, ‘] =
? ‘ ) ;
Readln( x[i] ) ;
END ;
interchange ;
Writeln ;
Writeln (' Số liệu đă sắp xếp :
') ;
Writeln ;
FOR i := 1 TO n DO
Writeln ( ‘x[ ‘, i : 3, ‘ ] =
‘, x[i] : 4 : 1 ) ;
Readln; END. Khi
chạy chương tŕnh, giả sử ta có 5
số liệu như phần nhập : (các
số có gạch dưới là phần nhập
từ bàn phím) Có
bao nhiêu phần tử số ?
5 x[
1] = ? 4.
7 x[
2] = ?
- 2. 3 x[
3] = ? 12.
9 x[
4] = ? 8.
8 x[
5] = ?
6. 0 Kết
quả là : Số
liệu đă sắp xếp : x[
1] = ? - 2. 3 x[
2] = ?
4. 7 x[
3] = ?
6. 0 x[
4] = ?
8. 8 x[
5] = ?
12. 9 Trong
một số bài toán thực tế, người
ta sử dụng các mảng nhiều hơn 1
chiều, gọi là mảng nhiều chiều. Ví
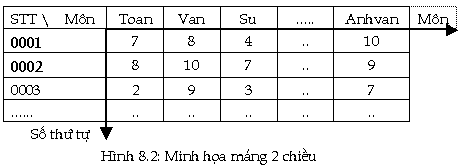
dụ 8.11: Pḥng
Đào tạo quản lư điểm của sinh viên.
Trong khoá 22 chẳng hạn, người ta tạo
ra một mảng 2 chiều: ví dụ một
chiều là số thứ tự của sinh viên,
chiều c̣n lại là các môn học (dạng
kiểu vô hướng liệt kê), ta có thể h́nh
dung dạng của mảng ghi điểm (tên
mảng là ghi_diem) như sau:
Lưu
ư: Thực tế, danh sách tên sinh viên lưu
lại trong máy tính thường được
ghi
bằng cách gán mă số sinh viên (coding) cho mỗi
sinh viên ngay từ năm đầu vào học. Với
ví dụ trên, muốn nhập điểm một
sinh viên nào đó ta phải khai báo 2 tham số là
số thứ tự sinh
viên và môn học.
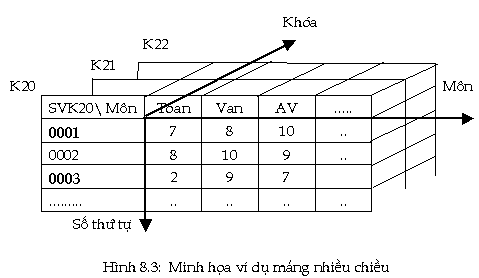
Tương tự, cũng với các khoá
kế tiếp theo học những môn như
vậy, ta sẽ tạo ra mảng nhiều
chiều như h́nh vẽ minh họa sau:
Trong trường hợp này, muốn biết
điểm một sinh viên nào đó ta phải
khai báo 3 tham số: Khoá học, số thứ
tự sinh viên và môn học, chẳng hạn: ghi_diem[K22,0001,AV]
nhập điểm 10,...
Khai báo cũng có 2 cách như đối
với mảng 1 chiều: +
Khai báo gián tiếp:
TYPE
<Kiểu mảng> = ARRAY
[Kiểu_chỉ_số_1, ...,
Kiểu_chỉ_số_n] OF <Kiểu phần
tử>;
VAR
<Danh sách biến>:<Kiểu mảng>; Ví
dụ 8.12:
TYPE matrix = ARRAY [1 .. 20, 1 .. 30] OF integer ;
VAR A:matrix; Lệnh
trên khai báo một kiểu tên matrix.
Đây là một mảng 2 chiều, chiều
thứ nhất có các chỉ số từ 1 đến
20, chiều thứ hai có các chỉ số từ 1
đến 30, tổng cộng ta có (20 x 30) phần
tử số nguyên. Và ta có một biến A là
biến có kiểu matrix. Ví
dụ trên cũng có thể được khai báo
tương đương với:
TYPE matrix = ARRAY [1 .. 20] OF ARRAY [1 .. 30] OF integer ;
VAR A:matrix; +
Khai báo gián tiếp:
VAR
<Danh
sách biến>: ARRAY
[Kiểu_chỉ_số_1, ...,
Kiểu_chỉ_số_n] OF <Kiểu phần
tử>;
Khai
báo một
biến A có 5 ḍng và 10 cột kiểu phần
tử là Integer như sau: VAR
A : ARRAY [1 .. 5, 1 .. 10] OF
integer ; +
Truy xuất các phần tử mảng: Tương
tự như cách truy xuất phần tử
của mảng 1 chiều, mảngg nhiều
chiều cũng được truy xuất thông
qua tên biến mảng kết hợp với các
chỉ số của
nó được đặt trong cặp dấu
ngoặc vuông. Mảng
2 chiều là một ma trận, như ví dụ trên
ta có một ma trận 5 ḍng và 10 cột. Các
phần tử của ma trận A được kư
hiệu là a[i,j] với i là vị trí cột và j
là ḍng. Khi viết a[2, 7] th́ hiểu đây là
phần tử ở ḍng 2 và cột 7. Trong
Pascal, ta có thể viết a[i,j] thành a[i] [j] với
ư nghĩa hoàn toàn như nhau. Chú
ư: Trên nguyên
tắc, ta có thể khai báo một mảng có
đến 255 chiều. Tuy vậy, một điều
cần lưu ư là kích thước bộ nhớ
của máy tính có hạn nên thường chỉ
khai báo mảng từ 1 đến 3 chiều. Khai
biến quá nhiều th́ phải cần máy lớn
hơn. Chẳng
hạn khi báo 1 mảng [1.. 10] các phần tử
số nguyên đă lấy 10 bytes bộ nhớ
- Mảng 2 chiều 10 x 10
= 100 bytes bộ nhớ.
- Mảng 3 chiều 10 x 10 x 10 = 1 000 bytes
bộ nhớ
- Mảng 4 chiều 10 x 10 x 10 x 10 = 10 000 bytes
bộ nhớ
- Mảng 5 chiều 10 x 10 x 10 x 10 x 10 = 100 000
bytes bộ nhớ
- v.v... Ví
dụ 8.13: Viết
một chương tŕnh Pascal để đọc
một bảng các số thực được
nhập vào máy tính dưới dạng một
mảng 2 chiều. Tính tổng các giá trị
số theo hàng và theo cột. Kết quả
được in ra màn h́nh theo vị trí hàng và
cột tương ứng. Trước
tiên, ta bắt đầu bằng định nghĩa
các biến: table
= mảng 2 chiều chứa số thực dưới
dạng bảng gồm các số nhập và
kết quả nrows
= một biến số nguyên chỉ số hàng ncols
= một biến
số nguyên chỉ số cột row
=
một số đếm nguyên chỉ số hàng col
= một số đếm nguyên chỉ
số cột Để
đơn giản, chúng ta giả sử rằng kích
thước số liệu nhập vào bảng tính
không vượt quá 10 hàng và 10 cột. Ta sẽ
thêm vào 1 hàng cộng phía dưới và 1 cột
cộng bên phải vào bảng để ghi
kết quả tính cộng các phần tử hàng
và cột tương ứng. Như vậy,
mảng 2 chiều của chúng ta sẽ trở thành
mảng sẽ được in ra có số hàng là
(nrows + 1) và số cột là (ncols +1). Do vậy, ta
phải khai báo biến table là 1 mảng 2 chiều
số nguyên có tối đa 11 cột và 11 hàng.
Để dễ theo dơi chương tŕnh, ta
thực hiện cấu trúc module khi viết chương
tŕnh bằng cách tiến hành làm các thủ
tục procedure cho đọc số liệu, tính
tổng các phần tử theo hàng, tính tổng các
phần tử theo cột và in ra màn h́nh bảng
kết quả. Các thủ tục này sẽ có tên
tương ứng là readinput, rowsums, columsums và
writeoutput.
Thuật toán logic yêu cầu cho mỗi
thủ tục là cách khai báo thẳng trước
(straightforward), chú ư rằng trong mỗi thủ
tục ta có một ṿng lặp đôi (double loop).
Ví dụ, để đọc số liệu
ở bảng gốc, ta sẽ phải làm một
ṿng lặp đôi sau: FOR
row := 1 TO nrows DO
BEGIN
FOR col := 1 TO ncols DO readln( table[row, col] ) ;
Writeln;
END ; Câu
lệnh Writeln để báo chương tŕnh
nhảy tới ḍng kế. Tương
tự, ṿng lặp sau được viết để
tính tổng các phần tử theo hàng: FOR
row := 1 TO nrows DO
BEGIN
table
[row, ncols + 1] :=
0 ;
FOR
col := 1 TO ncols DO table
[row, ncols + 1] := table [row, ncols + 1] + table [row, col];
END ; Tương
tự, cấu trúc ṿng lặp đôi cũng
được dùng để tính tổng các
phần tử cột và in ra bảng kết
quả cuối cùng.
Sau
đây là chương tŕnh Pascal của bài toán trên: PROGRAM
Tongbang ;
{đọc một bảng số, tính
tổng từng cột và hàng của cá bảng} VAR
row, col :
1 .. 11 ;
nrows, ncols :
1 .. 10 ;
table : ARRAY [1 .. 11, 1 .. 11]
OF real ; PROCEDURE
Rowsums ; {cộng
các phần tử theo cột bên trong mỗi hàng } BEGIN
FOR row := 1 TO nrows DO
BEGIN
table [row,ncols+1] := 0 ;
FOR col := 1 TO ncols DO
table[row, ncols+1] := table[row, ncols+1] + table[row,col];
END ; END
; PROCEDURE
Columnsums ; {cộng
các phần tử theo hàng bên trong từng cột
} BEGIN
FOR col := 1 TO ncols DO
BEGIN
table [nrows+1, col] := 0 ;
FOR row := 1 TO nrows DO
table[nrows+1,col] := table[nrows+1,col] + table[row,col];
END ; END
; PROCEDURE
Readinput ; {đọc
các phần tử của bảng } BEGIN
Write(' Nhập số hàng (1 .. 10)
? ')
;Readln(nrows) ;
Write(' Nhập số cột (1 .. 10)
? ')
;Readln(ncols) ;
FOR row := 1 TO nrows DO
BEGIN
Writeln (' Nhập số liệu hàng số ,
row :2') ;
FOR col := 1 TO ncols DO readln(table [row, col] ) ;
END ; END
; PROCEDURE
Writeoutput ; {
In ra bảng số liệu và kết quả tính
tổng } BEGIN
Writeln('Bảng số liệu và kết
quả tính tổng các phần tử theo hàng và
cột ');
Writeln(‘=============================================
‘);
Writeln;
FOR row := 1 TO nrows + 1 DO
BEGIN
FOR col := 1 TO ncols+1 DO Write (table [row,col] : 6 : 1) ;
Writeln;
END ; END
; BEGIN
{ Thân chương tŕnh chính }
Readinput ;
Rowsums ;
Columnsums ;
Writeoutput; END.
{ Chấm dứt chương tŕnh
} Giả
sử, ta có bảng số liệu sau :
2.5
-6.3
14.7 4.0
10.8 12.4
-8.2
5.5
-7.2
3.1
17.7 -9.1 Khi
chạy chương tŕnh, ta có (số có gạch
dưới là số của người thử chương
tŕnh): Nhập
số hàng (1 .. 10 ) ? 3 Nhập
số cột (1 .. 10) ? 4 Nhập
số liệu hàng số
1 2.5
-6.3
14.7
4.0 Nhập
số liệu hàng số 2 10.8
12.4
-8.2
5.5 Nhập
số liệu hàng số 3 -7.2
3.1
17.7
-9.1 Chương
tŕnh sẽ tính tổng các giá trị ở hàng và
cột, xong in ra màn h́nh kết quả: Bảng
số liệu và kết quả tính tổng các
phần tử theo hàng và cột 2.5
-6.3 14.7
4.0
14.9 10.8
12.4 -8.2
5.5
20.5 -7.2
3.1
17.7 -9.1
4.5 6.1
9.2
24.2 0.4
0.0 Ta
có thể kiểm tra kết quả ở các hàng
và cột. Một
chuỗi dữ liệu là một loạt các kư
tự được định nghĩa bằng
từ khoá STRING theo sau là số kư tự cực
đại có thể có của chuỗi kư tự.
String là một kiểu cấu trúc được
thêm vào trong Turbo Pascal. Chúng
ta có thể khai báo kiểu chuỗi kư tự
String gián tiếp hoặc trực tiếp. Khai báo
gián tiếp là khai kiểu trước rồi sau
đó mới khai báo biến. Cách khai báo trực
tiếp là khai thẳng biến số. Chiều dài
tối đa của chuỗi kư tự phải là
một hằng nguyên và được đặt
trong dấu ngoặc vuông [ ]. Trường hợp
không khai báo th́ chương tŕnh sẽ lấy giá
trị mặc nhiên là 255 kư tự +
Khai báo gián tiếp
TYPE
<Tên kiểu String> = STRING [hằng nguyên]
;
VAR
<Tên biến> : <Tên kiểu String> ; Ví
dụ 8.14: TYPE
TenSV = STRING [25] ; {định
độ dài tối đa là 25}
Diachi = STRING; {mặc
nhiên có độ dài tối đa là 255} VAR
HT : TenSV ;
DC : Diachi ;
+ Khai báo trực tiếp
<Tên biến>
: STRING
[hằng nguyên] ; Ví
dụ 8.15:
VAR
HT : STRING [25] ;
DC : STRING;
Chuỗi
kư tự sẽ chiếm số byte trong bộ
nhớ bằng số kư tự lớn nhất
đă khai báo trước cộng thêm 1 byte đầu
tiên chứa số kư tự hiện có của
chuỗi kư tự. Ví
dụ 8.16:
TYPE DH =
STRING[10] ;
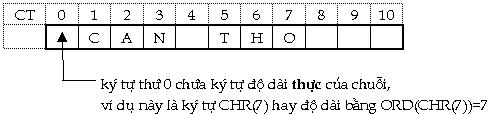
VAR CT :
DH ; và
nếu ta gán CT := CAN THO; th́
CT sẽ được cấp phát 1 + 10 = 11 ô
nhớ (byte) liên tục, với h́nh ảnh sau :
Chú
ư: -
Độ dài của chuỗi kư tự CT là 7 kư
tự mặc
dầu độ dài lớn nhất cho phép là 10. -
V́ ta dùng 1 byte để chứa chiều dài nên
string chỉ có tối đa là 255 kư tự. +
Phép gán Giống
như phép gán trong các kiểu vô hướng khác,
phép gán chuỗi là lệnh gắn một biến
với một biểu thức kư tự để
trong cặp dấu nháy đơn
<Tên biến> := Biểu thức kư tự
; Ví
dụ 8.17:
HT := Lê Văn Hai ;
DC := Số 12/4 đường Trần Hưng
Đạo, TP. Cần thơ ; +
Phép cộng Phép
cộng là thuật toán nối các chuỗi
lại với nhau bằng dấu cộng (+). Ví
dụ trên nếu ghép HT + DC th́ ta sẽ được: Lê
Văn Hai Số 12/4 đường Trần Hưng
Đạo, TP. Cần thơ Ghi
chú:
Không có phép trừ, nhân, chia trong chuỗi kư
tự. +
Các phép so sánh Các
so sánh gồm có bằng nhau =, lớn hơn >,
lớn hơn hoặc bằng >=, khác nhau <>,
nhỏ hơn <, nhỏ hơn hoặc bằng
<=
Khi so sánh 2 chuỗi kư tự th́ các kư
tự được so sánh từng cặp
một từ trái sang
phải theo giá trị của bảng mă ASCII. Có 2
khả năng xảy ra khi so sánh:
- Nếu 2 chuỗi có độ dài khác nhau
nhưng số kư tự giống nhau cho đến
độ dài chuỗi ngắn nhất th́
chuỗi ngắn nhỏ hơn chuỗi dài. Ví
dụ 8.18:
'Nation' < 'National'
'Lan' < 'Lang'
- Nếu 2 chuỗi có độ dài và
nội dung giống nhau th́ bằng nhau. Ví
dụ 8.19:
'Hello' =
'Hello'
Ghi
chú:
Chuỗi rổng (null string, viết là '') là
chuỗi không có chứa ǵ cả. Nó có giá
trị nhỏ hơn mọi string khác rỗng. V́
vậy:
'A' >''
và chr(32)>
'' +
Câu lệnh Read và Readln Hai
câu lệnh này đối với chuỗi cũng
tương tự như đối với các
kiểu vô hướng khác, nhưng cần lưu
ư:
- Lệnh Read và Readln chỉ cho phép đọc
tối đa 127 kư tự một chuỗi nhập
từ bàn phím mặc dầu chiều dài tối
đa của một chuỗi có thể đến
255 kư tự.
- Nếu ta đọc một lúc nhiều
biến theo kiểu Read(biến1, biến2, ...,
biếnN) ( hoặc Readln(biến1, biến2, ...,
biếnN)) th́ có thể bị nhầm lẫn khi
ta nhập giá trị có độ dài vượt
quá độ dài tối đa của biến1 th́
phần vượt sẽ được gán cho
biến2. Ngược lại, nếu ta nhập giá
trị ít hơn độ dài của biến1 th́
chương tŕnh lại lấy các giá trị
của biến2 gán thêm cho biến1 kể cả
khoảng trống. Do vậy, cách tốt nhất là
đối với biến kiểu String chỉ nên
nhập mỗi lần 1 biến. Ví
dụ 8.20:
Nên tránh viết kiểu Read(TenSV, Diachi); mà nên
viết :
Read(TenSV) ;
Read(Diachi) ;
hoặc:
Readln(TenSV) ;
Readln(Diachi) ;
- Độ dài thực tế của chuỗi là
độ dài thực tế khi ta đọc vào
từ bàn phím mặc dầu trước đó ta
có khai báo độ dài chuỗi. Nếu ta gơ Enter
mà không gơ kư tự nào trước đó th́
mặc nhiên chương tŕnh hiểu đó là
một chuỗi rỗng (null string hay st = ''). +
Câu lệnh Write và Writeln Tương
tự như trên nhưng cần một số lưu
ư về cách viết: -
Nếu
viết Write(st) hoặc Writeln(st) gọi là cách
viết không qui cách th́ mỗi kư tự sẽ
chiếm 1 vị trí trên màn h́nh. -
Nếu
viết Write(st : n) hoặc Writeln(st : n) gọi là cách
viết theo qui cách, với n là số nguyên, th́ màn
h́nh sẽ dành n vị trí để viết
chuỗi st theo lối canh trái nếu n> 0 và ngược
lại theo lối canh phải nếu n < 0. -
Một
số chuỗi mà trong đó có dấu như là
một chữ viết tắt, ví dụ như câu:
Hes an Intal staff (Ông ta là một nhân viên quốc
tế) th́ nơi có dấu phải viết thành (đây
là 2 dấu nháy đơn chứ không phải là
1 dấu nháy kép ). Ta
viết:
Writeln ( ‘ He ‘’s an Int’’al staff ‘) ; Chuỗi
kư tự được dùng khá phổ biến
trong lập tŕnh nên Turbo Pascal đă đưa
sẵn vào một số thủ tục và hàm
chuẩn để xử lư chuỗi kư tự. *
Thủ tục xóa DELETE (St, Pos, Num) Ư
nghĩa: Xóa
khỏi chuỗi St một số kư tự là Num
bắt đầu từ vị trí Pos tính từ
trái sang. Ví
dụ 8.21:
VAR st : string
[20];
Begin
St := ' BÀ BA BÁN BÁNH
B̉ '; Writeln (St) ;
DELETE (St, 10, 4); Writeln(St);
Readln ;
End. Khi
chạy chương tŕnh, ta sẽ thấy trên màn
h́nh: BÀ
BA BÁN BÁNH B̉ BÀ
BA BÁN B̉ *
Thủ tục INSERT (Obj, St, Pos) Ưï
nghĩa: Chèn chuỗi Obj xen vào chuỗi St kể
từ vị trí Pos tính từ bên trái. Ví
dụ 8.22:
VAR st : string
[25];
Begin
St := 'BÀ BA BÁN
BÁNH B̉' ; Writeln
(St) ;
INSERT ( BỤNG BỰ
, St, 6); Writeln(St);
Readln ;
End. Khi
chạy chương tŕnh, ta sẽ thấy trên màn
h́nh: BÀ
BA BÁN BÁNH B̉ BÀ
BA BỤNG BỰ BÁN BÁNH B̉ *
Thủ tục STR (S [: n[: m]], St) Ư
nghĩa: Đổi giá trị số S thành chuỗi
rồi gán cho St, Giá trị n:m nếu có sẽ là
số vị trí và số chữ số thập phân
của S. Ví
dụ 8.23:
VAR S:
real;
St: string[10];
Begin
S:= 12345.6718;
Writeln(S:5:2);
Str(S:6:2:st);
Readln;
End. Kết
quả trên màn h́nh:
12345.67
{Đây là số }
12345.67
{Đây là chuỗi} *
Thủ tục VAL(St, S, Code) Ư
nghĩa: Đổi
chuỗi số St (biểu thị một số
nguyên hoặc số thực) thành số (số
nguyên hoặc số thực) và gán giá trị này
cho S. Code là số nguyên dùng để phát
hiện lỗi: nếu đổi đúng th́ Code
có giá trị = 0, nếu sai do St không biểu
diễn đúng số nguyên hoặc số
thực th́ Code sẽ nhận giá trị bằng
vị trí của kư tự sai trong chuỗi St. Ví
dụ 8.24:
VAR
St : String[10];
SoX : real;
maloi: integer;
Begin
St:= ‘123.456’ ;
VAL(St,SoX,maloi) ;
Writeln('Số X = ,
SoX :5:2, và mă lỗi = , maloi) ;
Readln;
St:=‘123.XXX ’;
VAL(St,SoX,maloi);
Writeln('St = 123.XXX không đổi thành số
được !');
Writeln('Sai lỗi ở vị trí thứ
' , maloi); Readln;
End. Khi
chạy, ta sẽ thấy trên màn h́nh: 123.45
và maloi = 0 St
= 123.XXX không đổi thành số được
! Sai
lỗi ở vị trí thứ 5 *
Hàm LENGTH (St) Ư
nghĩa: Cho kết quả là một số nguyên
chỉ độ dài của chuỗi kư tự St. Để
viết 1 chuỗi kư tự ở trung tâm màn h́nh,
ta có thể dùng thủ thuật viết chuỗi
là (80 - lenght(st)) div 2 Ví
dụ 8.25:
Uses CRT;
Var
St : String[80];
Begin
ClrScr ;
Write(' Nhập vào một câu : ');
Readln(St) ;
Gotoxy(80 - Lenght(St)) div2, 12); Writeln(St)
;
Readln ;
End. *
Hàm COPY (St, Pos, Num) Ư
nghĩa: Cho
kết quả là một chuỗi kư tự mới
có được bằng cách chép từ chuỗi
St, bắt đầu từ vị trí Pos và chép
Num kư tự.
Nếu vị trí Pos lớn hơn chiều dài
của chuỗi St th́ hàm COPY sẽ cho một
chuỗi rỗng. Nếu giá trị của vị
trí Pos và số kư tự Num (Pos + Num) lớn hơn
chiều dài của chuỗi St th́ hàm COPY chỉ
nhận các kư tự nằm trong chuỗi St. Ví
dụ 8.26:
Var
St1, St2 : string[25] ;
Begin
St1 := ‘UNIVERSITY OF CANTHO : 1966 - 1996’ ;
St2 := COPY (St1, 15, 6) ;
End. Như
vậy, giá trị của biến St2 bây giờ là
CANTHO. *
Hàm CONCAT (St1, St2, ..., StN) Ư
nghĩa: Cho
kết quả là một chuỗi mới được
ghép theo thứ tự từ các chuỗi St1, St2,
..., StN. Hàm này giống như phép cộng các
chuỗi. Chuỗi mới cũng sẽ không
được vượt quá 255 kư tự. *
Hàm POS (Obj, St) : Ư
nghĩa: Cho
kết quả là vị trí đầu tiên của
chuỗi Obj trong chuỗi St. Nếu không t́m
thấy th́ hàm POS cho giá trị 0. Ví
dụ 8.27: nếu
St := 1234567890, nếu Obj := 456 th́ POS (Obj, St) = 4 c̣n
POS(4X, St)=0 d.
Truy xuất từng kư tự trong chuỗi Ta
có thể truy xuất đến từng kư tự
trong chuỗi với tên biến và chỉ số
trong dấu ngoặc vuông [ ] như truy xuất các
phần tử của mảng. Ví dụ với
chuỗi St th́ St[i] là kư tự thứ i trong
chuỗi St, dĩ nhiên Ví
dụ 8.28:
Program
DoiChu;
Var
St:String; i:
integer;
Begin
Write('Hăy nhập tên của bạn : '); Readln(St);
FOR i:= 1 TO Length(St) DO
St[i] := Upcase(St[i]);
(*Hàm Upcase
đổi kư tự thành chữ in hoa*)
Writeln;
Writeln(St); Readln;
End. Một
tập hợp (SET) bao gồm một số các
phần tử có cùng bản chất kiểu là
kiểu cơ bản. Trong Turbo Pascal và IBM Pascal,
số phần tử tối đa trong một
tập hợp là 256. Kiểu cơ bản có
thể là kiểu vô hướng liệt kê,
kiểu miền con hoặc kiểu Char, không
được là số thực. Khái niệm
tập hợp trong Pascal tương tự như
khái niệm tập hợp trong toán học.
+ Khai báo gián tiếp
TYPE
<Kiểu cơ bản> =
(phần_tử_1, phần_tử_2, ...,
phần_tử_n) ;
<Tên kiểu tập hợp> = SET OF
<Kiểu cơ bản> ;
VAR
<Tên biến > : <Tên kiểu tập
hợp> ; Ví
dụ 8.29:
TYPE
Sizes =
(short, medium, large) ;
Shirtsizes = SET OF sizes ;
VAR
shortleeve, longleeve : shirtsizes ;
+ Khai báo trực tiếp
VAR
<Tên biến> :
SET OF <Kiểu cơ bản> ;
Ví
dụ 8.30:
VAR
Chu :
SET OF Char ;
So
: SET OF 0 .. 9 ;
ABC :
SET OF 0 .. 256 ;
Date :
SET OF (Sun, Mon, Tue, Wed, Fri, Sat) ; Một
tập hợp được mô tả bằng cách
liệt kê các phần tử của tập
hợp, chúng cách nhau bằng một dấu
phẩy (,) và được đặt giữa
hai dấu móc vuông [ ], các phần tử có
thể là hằng, biến hoặc biểu
thức. Ví
dụ 8.31:
[]
{tập
hợp rỗng, không có các phầnt tử }
[5 .. 15]
{tập
hợp các chữ số nguyên từ 5 đến
15}
[1, 3, 5]
{tập
hợp 3 số 1, 3 và 5 }
[Hồng, Lan, Cúc, Mai]
{tập hợp tên 4 loài hoa} [i,
i + j*2, 4, 5]
{tập hợp các biến nguyên gồm
số 4, 5 và a.
Phép gán Ta
có thể gán giá trị các tập đă
được mô tả vào các biến tập cùng
kiểu. Riêng tập hợp rỗng có thể gán
cho mọi biến kiểu tập hợp khác nhau. Với
ví dụ trên, ta có thể gán :
Chu :=
[X,Y,Z] ;
So
:= [2,3,4] ;
Date := []
; Nếu
ta viết Chu := [1,2]; th́ không hợp lệ v́ Chu là
tập hợp các chữ. Hợp
của 2 tập hợp A và B là một tập
hợp chứa tất cả các phần tử
của tập A hoặc B hoặc cả A và B. Kư
hiệu của phép hợp là dấu cộng (+).
Phép hợp có tính giao hoán: A+B
= B+A Ta
có thể mô tả phép hợp qua h́nh ảnh sau :
Ví
dụ 8.32
A := [0,1,3,5,7,9] ;
B := [0,2,4,6,8,9]
;
C := A + B ;
{tập hợp C sẽ có các phần tử
là [0,1,2,3,4,5,6,7,8,9] } c.
Phép giao Giao
của 2 tập hợp A và B là một tập
chứa các phần tử của cả A và
cả B. Kư
hiệu A * B. Phép giao cũng có tính giao hoán, nghĩa
là A * B = B * A Minh
họa như sau :
Với
ví dụ trong phép hợp, nếu:
D := A * B ;
{tập D chứa phần tử [0,9] } Nếu
A và B không có phần tử nào giống nhau th́ phép
hợp sẽ cho tập rỗng. d.
Phép hiệu Hiệu
của 2 tập hợp A và B, kư hiệu là A - B, là
một tập hợp chứa các phần tử
chỉ thuộc A mà không thuộc B. Lưu ư :
A - B th́ khác B - A. Ví
dụ 8.33:
A := [3 .. 7] ;
B := [1.. 6, 10,
15] ;
th́
A - B là tập hợp [7] c̣n B - A là tập
hợp [1,2, 10,15] Phép
thuộc IN cho phép thử xem một giá trị nào
đó thuộc về một tập hay không? Phép
thuộc IN cho kết quả có kiểu Boolean.
Nếu đúng nó sẽ cho kết quả là TRUE,
ngược lại là FALSE. Ví
dụ 8.34:
Chu là biến kiểu Char, c̣n A là biến
kiểu SET OF Char và
Chu := ‘X’ ;
A :=
[‘X’, ‘x’,’Y’, ‘y’, ‘Z’, ‘z’] ;
th́ phép toán Chu IN A sẽ cho kết quả là
TRUE f.
Các phép so sánh =, <>, <= và >= Muốn
so sánh 2 tập hợp với nhau th́ chúng phải
có cùng kiểu cơ bản. Kết quả
của các phép so sánh là giá trị kiểu Boolean,
tức là TRUE (Đúng) hoặc FALSE (Sai).
Hai tập hợp A và B gọi là bằng nhau
(A = B) chỉ khi chúng có các phần tử
giống với nhau từng đôi một (không
kế thứ tự sắp xếp các phần
tử trong 2 tập). Ngược lại của phép
so sánh bằng nhau (=) là phép so sánh khác nhau
(<>). Nghĩa là, nếu A = B là TRUE th́ A <>
B sẽ là FALSE và ngược lại.
Phép so sánh nhỏ hơn hoặc bằng
(<=) của A <= B sẽ cho kết quả là
TRUE nếu mọi phần tử có trong A đều
có trong B. Định nghĩa này cũng tương
tự như lớn hơn hoặc
bằng (>=). Với A >= B th́ mọi phần
tử của B đều có trong A, kết quả
này TRUE, ngược lại là FALSE. Chú
ư: Trong Pascal không có phép so sánh nhỏ hơn (<)
và lớn hơn (>). Để kiểm tra xem
tập A có thực sự nằm trong tập B hay
không (A nhỏ hơn B), ta phải sử dụng
thêm các phép logic như sau: IF (A <> B) AND (A <= B) THEN WRITELN ( ‘A < B’)
Với
dữ liệu kiểu tập hợp, ta không
thể viết ra hoặc đọc vào bằng các
thủ tục (Write) Writeln hoặc (Read) Readln. Tuy
nhiên, ta có thể thực hiện các thao tác này
khi mà kiểu cơ bản của tập hợp là
số nguyên, kư tự. Ví
dụ 8.35: Viết
chương tŕnh để đọc một câu
bất kỳ, sắp xếp các chữ của câu
đó theo thứ tự
ABC abc từ chữ in đến chữ thường.
Chương tŕnh chấm dứt khi nhận
được chữ END hoặc end. PROGRAM
Letters_used ; TYPE
letters = SET OF char ; VAR
used, unused : letters ;
count, charcount : 0 .. 80 ;
alpha : char ;
line : string ; PROCEDURE
Readinput ; {đọc
một câu bất kỳ} BEGIN
FOR count := 1 TO 80 DO line[count]
:= ‘ ‘ ;
Writeln (' Nhập vào một ḍng câu dưới
đây : ') ;
Count := 0;
WHILE NOT eoln DO {hàm eoln trả về giá
trị false khi kư
tự nhận vào khác}
BEGIN
{kư tự kết thúc ḍng CR: carry return}
count := count + 1 ;
read(line[count]);
END ;
readln;
charcount := count; END
; PROCEDURE
Writeoutput ; {tŕnh
bày phân tích của một ḍng câu } BEGIN
writeln;
write(' Các chữ đă sử dụng:
') ;
FOR alpha := ‘A’ to ‘z’ DO
IF [alpha] <= used THEN write( ‘
‘, alpha) ;
writeln;
writeln; END; BEGIN
{Thân chương tŕnh chính}
Readinput;
WHILE NOT (([line[1]] <= [‘E’, ‘e’])
AND ([line[2]] <= [‘N’, ‘n’])
AND ([line[3]] <= [‘D’, ‘d’]))
DO
BEGIN
used := [] ;
unused := [‘A’ .. ‘Z’, ‘a’ .. ‘z’] ;
FOR count := 1 TO charcount DO
IF [line[count]] <= unused THEN
BEGIN
used := used + [line[count]] ;
unused := unused - [line[count]];
END ;
Writeoutput ;
Readinput;
END ; END. Khi
chạy chương tŕnh, ta sẽ thấy (Các ḍng
chữ gạch dưới là của người
dùng): Nhập
vào một ḍng câu dưới đây: Pascal
is a structured programming language derived from ALGOL - 60
Các
chữ đă sử dụng:
A G L O P a c d e f g i l m n o p r s t u v Nhập
vào ḍng câu dưới đây: END Các
cấu trúc dữ liệu kiểu mảng (Array) và
tập hợp (Set) có hạn chế ở chỗ
các phần tử trong tập hợp của chúng
phải cùng kiểu mô tả. Song trong thực
tế, có những kiểu cấu trúc dữ
liệu khác nhau nhưng lại có một mối
liên quan nào đó. Ví
dụ 8.36: Để
mô tả dữ liệu về lư lịch một
người nào đó, người ta phải khai
báo họ tên người (kiểu String), Phái (Nam
:=True, Nữ := False theo kiểu Boolean), ngày sinh (mô
tả kiểu date), địa chỉ (kiểu
String) và mức lương (kiểu integer), v.v...
Với các kiểu cơ bản khác nhau như
vậy trong Pascal, ta phải dùng kiểu bản ghi
(RECORD). Kiểu
bản ghi trong ngôn ngữ Pascal gắn liền
với kiểu tập tin (FILE) - sẽ được
tŕnh bày trong phần kế tiếp.
Tuy nhiên, ta có thể sử dụng RECORD
một cách độc lập với FILE.
RECORD là kiểu dữ liệu bao gồm
nhiều thành phần có thể khác nhau về
kiểu dữ liệu, mỗi thành phần
được gọi là trường (Field). Cú
pháp khai báo kiểu bản ghi (Record) trước
rồi khai báo biến như sau: +
Khai báo gián tiếp:
<Tên kiểu bản ghi> = RECORD
<Tên trường 1a>[,<Tên trường1b>,...]
: <Kiểu trường> ;
<Tên trường 2a>[,<Tên trường2b>,...]
: <Kiểu trường> ;
..............................................................................................
;
END ; VAR <Tên biến1>[,<Tên biến2>, ...] : <Tên kiểu bản ghi> ; Ví
dụ 8.37:
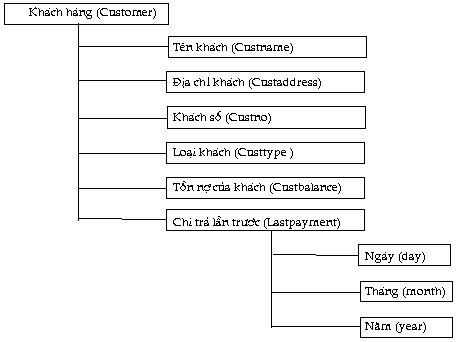
Ta
đang làm một khai báo về khách hàng của công
ty chuyên bán hàng trả góp nào đó. Số
liệu cần sử dụng là ngày tháng làm
bản ghi và các thông tin cơ bản về khách
hàng nợ thanh toán cho công ty, theo minh họa ở
h́nh dưới:
Trong chương tŕnh này, Công ty phân ra 3 t́nh
trạng loại khách nợ (status): đúng kỳ
hạn phải trả (current), đă quá hạn
phải trả (overdue) và loại khách chểnh
mảng, dây dưa việc trả nợ nhiều
lần (delinquent). Ở đây: -
Status được khai báo theo kiểu dữ
liệu liệt kê (enumerated data type). -
Account (Số kế toán) là một kiểu record,
chứa các thông tin về tên và địa
chỉ khách nợ (kiểu chuỗi string), số
khách nợ (kiểu số nguyên integer-type),
loại khách nợ (kiểu liệt kê enumerated
type) và số liệu tồn đọng nợ
của khách (kiểu số thực real-type). -
Date (Ngày tháng) là một kiểu Record trong chương
tŕnh ghi ngày, tháng năm đáo nợ của khách
hàng. Biến
của chương tŕnh là khách hàng (customer). Ta
có thể khai báo như sau:
TYPE status
= (current,
overdue, delinquent);
date =
RECORD
day : 1 .. 31 ;
month : 1 ..12 ;
year : 1900 .. 2100 ;
END
;
account = RECORD
Custname : String ;
Custaddress : String ;
Custno : 1 .. 9999 ;
Custtype : status ;
Custbalance : Real ;
Lastpayment : date;
END;
VAR customer
: account ;
+ Khai báo
trực tiếp
VAR
<Tên
biến1>[,<Tên biến2>, ...] : RECORD
<Tên trường 1a>[,<Tên trường1b>,...]
: <Kiểu trường> ;
<Tên trường 2a>[,<Tên trường2b>,...]
: <Kiểu trường> ;
..............................................................................................
;
END ; Để
truy xuất vào một trường của
kiểu Record, ta cần dùng tên biến kiểu
Record, sau đó là dấu chấm (.) rồi đến
tên trường. Dạng tổng quát sau: Ví
dụ 8.39:
Nhập lư lịch nhân viên của một cơ
quan TYPE
Lylich = RECORD
{Lư lịch gồm Họ tên, Tuổi, Phái, Lương}
Hoten : string [25] ;
Tuoi : integer ;
PhaiNam : boolean;
{Nam : M (Male), Nữ : F (Female)}
Luong : real;
END; VAR
x, y : Lylich ; nv
: ARRAY [1 .. 200] OF Lylich ;
{nv là mảng lư lịch các nhân viên} ..................................
Write('Nhập tổng số nhân viên :
'); readln(n) ;
FOR i := 1 TO n
DO
BEGIN
Write(' Họ tên : '); readln(nv[i].Hoten);
Writeln(' Tuổi : '); readln(nv[i].Tuoi) ;
Write(' Phái (Nam :M, Nữ : F) ? '); readln (Phai);
IF (Phai = ‘M’) or (Phai =‘m’) THEN nv[i].PhaiNam :=
TRUE
ELSE nv[i].PhaiNam := FALSE ;
Writeln(' Lương : '); read(nv[i].Luong) ;
END ; ....................................... Lưu
ư : ·
Các
biến Record có thể gán cho nhau. Ví dụ x và y
là 2 biến bản ghi có cùng kiểu Lylich, th́ ta
có thể gán:
x := y; Như
vậy ta không phải lặp lại:
x.Hoten := y.Hoten ;
x.Tuoi := y.Tuoi ;
................................. ·
Không
được viết ra màn h́nh hoặc đọc
từ bàn phím một biến record như :
Writeln(x);
hoặc Readln(x); ·
Không
thể so sánh các record bằng các phép toán quan
hệ <, >, <=, >=,=,<> ·
Không
được dùng các toán số học và logic
với kiểu record. Ví
dụ 8.40: Nhập
vào 2 số phức C1 và C2 và tính C3 là tổng
của chúng Với
chương tŕnh loại này ta phải lần lượt
nhập từng phần thực và phần ảo
riêng rẽ của C1 và C2. Ta không thể dùng ḍng
lệnh C3 = C1 + C2. Kết quả tính C3 phải là
phép cộng riêng rẽ từng phần thực và
phần ảo của C1 và C2 rồi ghép lại. PROGRAM
So_Phuc ; TYPE
Sophuc
= Record
pt, pa : real ;
End; VAR
c1,
c2, c3 : Sophuc ; BEGIN
Write('Lần lượt nhập phần
thực và phần ảo của 2 số phức
C1 và C2') ;
Write('Nhập phần thực của số
phức C1 : ') ; Readln(c1.pt) ;
Write('Nhập phần ảo của số
phức C1 : ') ; Readln(c1.pa) ;
Write('Nhập phần thực của số
phức C2 : ') ; Readln(c2.pt) ;
Write('Nhập phần ảo của số
phức C2: ') ; Readln(c2.pa) ;
c3.pt := c1.pt + c2.pt ;
c3.pa := c1.pa + c2.pa ;
Writeln('Kết quả của phép cộng 2
số phức :');
Write(‘C3 = C1 + C2 ‘);
Write(‘
= (‘, c1.pt:5:2, ‘+i ‘, c1.pa:5:2, ‘) +(‘,
c2.pt:5:2, ‘+i ‘,c2.pa:5:2, ‘) ‘);
Write(‘C3 = ‘, c3.pt:5:2, ‘+i’, c3.pa:5:2 );
Readln; END.
Record lồng nhau là record mà có trường
(field) của nó lại có kiểu là một record
khác. Ta có thể định nghĩa các record
lồng nhau theo một cách trực tiếp hay gián
tiếp nhau và cách khai báo cũng hoàn toàn tương
tự như cách khai báo record ở trên. Ví
dụ 8.41: TYPE
dd_mm_yy = Record
dd:1..31;
mm:1..12;
yyyy:1900..2100;
end; hoso
=
Record
masv:string[7];
ngsinh:dd_mm_yyyy;
diem:real; end;
VAR
Lop: Array[1..20] of hoso; Nhiều
chương tŕnh đ̣i hỏi các phần tử
khác nhau của cùng một record phải được
thao tác tại các vị trí khác nhau bên trong chương
tŕnh. Như vậy phải cần có nhiều
chỉ thị trường khác nhau đặc trưng.
Việc này làm chương tŕnh trở nên
phức tạp, tẻ nhạt và khó theo dơi. Để
giải quyết t́nh trạng này, Pascal đă
đưa ra cấu trúc câu lệnh WITH ... DO
trong record nhằm bớt đi các rắc
rối từ các chỉ thị trường (hay nói
cách khác, câu lệnh WITH .. DO như là phép toán
đặt thừa số chung mà ở đó
thừa số chung là các tên biến record).
Dạng tổng quát của câu lệnh WITH là:
WITH <tên biến record> DO
BEGIN
<Câu lệnh với tên trường 1>;
.............................................
;
<Câu lệnh với tên trường n>;
END
; Ví
dụ 8.42: Một
biến bản ghi DANSO có các trường KHUVUC,
HOTEN, NGAYSINH, DIACHI, NGHE đưa
dữ liệu từ bàn phím như sau:
WITH DANSO
DO
BEGIN
Write ('Khu vực điều tra :'); Readln
(KHUVUC);
Write ('Họ tên công dân :'); Readln (HOTEN);
Write ('Ngày-tháng-năm sinh :'); Readln (NGAYSINH);
Write ('Địa chỉ công dân :'); Readln (DIACHI);
Write ('Nghề nghiệp : '); Readln (NGHE);
END ; Đối
với bản ghi có nhiều thứ bậc:
R1 là biến bản ghi có trường R2
R2 là biến bản ghi con có trường R3
R3 là biến bản ghi con có trường R4
..................... th́ câu lệnh WITH được tổ chức lồng nhau:
WITH R1 DO
WITH R2 DO
...............
WITH RN DO <Câu lệnh ...> ; hay
viết đơn giản hơn:
WITH Record1,
Record2, ..., RecordN DO <Câu lệnh BEGIN .. END> ; Ở
ví dụ 8.41, ta có thể viết như sau:
WITH Lop[i] DO
Begin
With Ngsinh Do
Begin
dd:= 25; mm:=05;
yyyy:=1978; End;
masv:='7962343'; diem:=9.0; End; |