|
BÀI ÐỌC THÊM LẬP TRÌNH THEO CẤU TRÚC TRÊN - XUỐNG.
Khi
lập trình, chúng ta thường có những đoạn
chương trình hay phép tính lặp lại
nhiều lần. Nếu mỗi lần lặp
lại, ta phải viết những đoạn
lệnh như nhau thì chương trình của chúng
ta trở nên dài dòng, rối rắm và mất
thời gian vô ích. Ðể giải quyết
những trường hợp như vậy, Pascal
cho phép chúng ta tạo ra các module, mỗi module mang
một đoạn chương trình gọi là chương
trình con (subroutine hay subprogram). Mỗi chương
trình con sẽ mang một cái tên khác nhau. Một
module chỉ cần viết một lần và sau
đó chúng ta có thể truy xuất nó nhiều
lần, bất kỳ nơi nào trong chương
trình chính. Khi
cần thiết, chúng ta chỉ việc gọi tên
chương trình con đó ra để thi hành
lệnh.
Nhờ sử dụng chương trình con, chương
trình có thể tiết kiệm được ô
nhớ. Ðồng thời, ta có thể kiểm tra tính
logic trong tiến trình lập trình cho máy tính điện
tử, có thể nhanh chóng loại bỏ những
sai sót khi cần hiệu chỉnh hay cải
tiến chương trình. Ðây là khái niệm cơ
bản trong ý tưởng lập chương trình
có cấu trúc. Một quá trình tính cũng có
thể có nhiều chương trình con lồng ghép
vào nhau.
Trong Pascal, chương trình con được
viết dưới dạng thủ tục
(procedure) và hàm
(function). Cấu trúc của 2 kiểu chương
trình con này thì tương tự với nhau,
mặc dầu cách truy xuất của chúng có
khác nhau và cách trao đổi thông tin trong mỗi
kiểu cũng có điểm khác nhau. Hàm (function)
trả lại một giá trị kết quả vô
hướng thông qua tên hàm và hàm được
sử dụng trong biểu thức.
Ví dụ hàm chuẩn, như hàm sin(x) mà chúng
ta đã biết trong chương trước có
thể được xem như một chương
trình con kiểu function với tên là sin và tham
số là x. Trong khi đó, thủ tục (procedure)
không trả lại kết quả thông qua tên
của nó, do vậy, ta không thể viết các
thủ tục trong biểu thức. Các lệnh
Writeln, Readln trong chương trước được
xem như các thủ tục chuẩn.
Một chương trình có chương trình
con tự thiết lập có 3 khối (block) :
* Khối khai báo
* Khối chương trình con
* Khối chương
trình chính *
Một số khái niệm biến: ·
Biến toàn cục (global variable): Còn được
gọi là biến chung, là biến được
khai
báo ở đầu chương trình, nó
được sử dụng bên trong chương
trình chính và cả bên trong chương trình con.
Biến toàn cục sẽ tồn tại trong
suốt quá trình thực hiện chương trình. ·
Biến
cục bộ (local variable): Còn được
gọi là biến riêng, là biến được
khai báo
ở đầu chương trình con, và nó
chỉ được sử dụng bên trong thân
chương trình con hoặc
bên trong thân chương trình con khác nằm bên
trong nó (các chương
trình con lồng nhau). Biến cục bộ chỉ
tồn tại khi chương
trình con đang hoạt động, nghĩa là
biến cục bộ sẽ được
cấp phát bộ nhớ khi chương trình con
được gọi để thi hành, và nó
sẽ được giải phóng ngay sau khi chương
trình con kết thúc. ·
Tham
số thực (actual parameter) là một tham số mà
nó có thể là một biến
toàn cục, một biểu thức hoặc
một giá trị số (cũng có thể
biến cục bộ khi sử dụng chương
trình con lồng nhau) mà ta dùng chúng khi truyền giá
trị cho các tham số hình thức tương
ứng của chương trình con. ·
Tham
số hình thức (formal parameter) là các biến
được khai báo ngay sau
Tên
chương trình con, nó dùng để nhận giá
trị của các tham số thực truyền
đến. Tham số hình thức cũng là
một biến cục bộ, ta có thể xem nó như
là các đối số của hàm toán học. *
Lời gọi chương trình con (thủ tục
và hàm):
Ðể chương rrình con được
thi hành, ta phải có lời gọi đến chương
trình con, lời gọi chương trình con thông
qua tên chương trình con và danh sách các tham
số tương ứng (nếu có).
Các qui tắc của lời gọi chương
trình con: ·
Trong
thân chương trình chính hoặc thân chương
trình con, ta chỉ có
thể gọi tới các chương trình con
trực thuộc nó. ·
Trong
chương trình con, ta có thể gọi các chương
trình con ngang cấp đã được thiết
lập trước đó. Thủ
tục là một đoạn cấu trúc chương
trình được chứa bên trong chương
trình Pascal như là một chương trình con.
Thủ tục được đặt tên và có
thể chứa danh sách tham số hình thức
(formal parameters). Các tham số này phải được
đặt trong dấu ngoặc đơn ( ). Ta có
thể truy xuất thủ tục bằng cách
gọi tên của thủ tục. Chương trình
sẽ tự động truy xuất thủ
tục đúng tên đã gọi và thực
hiện các lệnh chứa trong thủ tục
đó. Sau khi thực hiện thủ tục xong, chương
trình sẽ trở lại ngay lập tức sau
vị trí câu lệnh gọi thủ tục đó.
Có 2 loại thủ tục: +
thủ tục không tham số +
và thủ tục có tham số. a.
Cấu trúc của thủ tục không tham số
PROCEDURE < Tên thủ tục > ;
{ Các khai báo hằng, biến, kiểu cục
bộ... }
BEGIN
{ ... các lệnh trong nội bộ thủ
tục ... }
END ; Ví
dụ 7.1:
Tìm số lớn nhất trong 3 trị số
nguyên PROGRAM
Largest ; (* Xác định số lớn
nhất trong 3 trị số nguyên được
nhập vào *) VAR
a, b, c : integer ;
yn : char ;
PROCEDURE maximum
;
VAR max
: integer ;
BEGIN
IF a > b THEN
max := a
ELSE max := b ;
IF c > max THEN max := c ;
Writeln (' Số lớn nhất là'
, max ) ;
END ; BEGIN
(* Ðoạn chương trình chính
*)
yn :=
‘Y‘ ;
WHILE ( upcase(yn) = ‘Y ‘)
DO
BEGIN
Writeln
(' Nhập 3 số nguyên : ') ;
Readln
(a, b, c ) ;
maximum ;
(* --- Lời gọi thủ tục maximum --- *)
Write ('
Tiếp tục nhập 3 số mới không (y/n) ?
') ;
Readln
(yn) ;
END ; END.
Chú
ý:
Trong chương trình trên, thủ tục
maximum được khai báo trước khi nó
được truy xuất, các biến a, b, c
được gọi nhập vào ở chương
trình chính và biến max được định
nghĩa bên trong thủ tục. Ðiều này cho ta
thấy, không phải lúc nào cũng cần
thiết khai báo biến ngay đầu chương
trình chính.
PROCEDURE < Tên thủ tục > (<danh sách
tham số hình thức : kiểu biến>);
{ Các khai báo hằng, biến, kiểu cục
bộ ... }
BEGIN
{ ... các lệnh trong nội bộ thủ
tục ... }
END ;
Khi viết một thủ tục, nếu có các
tham số cần thiết, ta phải khai báo nó
(kiểu, số lượng, tính chất, ...). Các
tham số này gọi là tham số hình thức
(formal parameters).
Một thủ tục có thể có 1 hoặc
nhiều tham số hình thức. Khi các tham số hình
thức có cùng một kiểu thì ta viết chúng
cách nhau bởi dấu phẩy (,). Trường
hợp các kiểu của chúng khác nhau hoặc
giữa khai báo tham số truyền bằng tham
biến và truyền bằng tham trị (sẽ
học ở phần sau ) thì ta phải viết cách
nhau bằng dấu chấm phẩy (;). Ví
dụ 7.2: Tính
giai thừa của một số PROGRAM
Tinh_Giai_thua ; VAR
n : integer ; gt : real ; {các biến chung}
PROCEDURE giaithua
(m : integer );
VAR i
: integer ; {i là
biến riêng}
BEGIN
gt := 1 ;
FOR i := 1 TO m DO gt := gt * i ;
END ; BEGIN
(* Thân chương trình chính *)
Write('Nhập số nguyên
n (0 <= n < 33) =
') ; Readln (n) ;
If n>=0 then
Begin
giaithua (n) ;
Writeln ('Giai thừa của , n, là :'
, gt: 10 : 0) ;
End
Else Writeln('
Không tính giai thừa của một số âm! ') ;
Readln; END.
Trong
chương trình trên m là các tham số hình
thức của thủ tục giaithua.
Khi gọi thủ tục giaithua (n) thì tham
số thực n được truyền tương
ứng cho tham số hình thức m. Ví
dụ 7.3: Giải
phương trình ax2 + bx + c = 0, theo dạng chương
trình con lồng nhau: PROGRAM
Giai_PTB2; VAR
hsa, hsb, hsc:real;
{các biến toàn cục}
PROCEDURE Ptb2(a,b,c:real);
{a, b, c là các tham số hình thức của
Ptb2}
Var
delta:real; {biến
cục bộ}
PROCEDURE Ptb1(a1,b1:real);
{a,b là các tham số hình thức của Ptb1}
Begin
if a1=0 then
if
b1=0 then
writeln('Phương
trình vô số nghiệm')
else
writeln('Phương trình vô nghiệm')
else
writeln('Phương trình có nghiệm
=',-b1/a1:8:2);
End; {kết
thúc thủ tục Ptb1}
Begin {bắt
đầu thủ tục Ptb2} (3)
if
a=0 then ptb1(b,c) {b,
c là các tham số thực cho Ptb1} (4)
else
begin
delta:=sqr(b)-4*a*c;
if delta>0 then
begin
writeln('Nghiệm
x1= ',(-b+sqrt(delta))/(2*a):8:2);
writeln('Nghiệm x2= ',(-b-sqrt(delta))/(2*a):8:2);
end
else
if delta=0 then
writeln('Nghiệm
kép x1=x2= ',-b/(2*a):8:2)
else
writeln('delta <0
=> Phương trình vô nghiệm');
end;
End;
{kết thúc thủ tục Ptb2} Begin
{chương trình chính} (1)
write('Nhập các hệ số a, b, c =
');readln(hsa, hsb, hsc); (2)
Ptb2(hsa,hsb,hsc);
{hsa, hsb, hsc là các tham số thực cho Ptb2} (5)
readln; End.
{kết thúc chương trình}
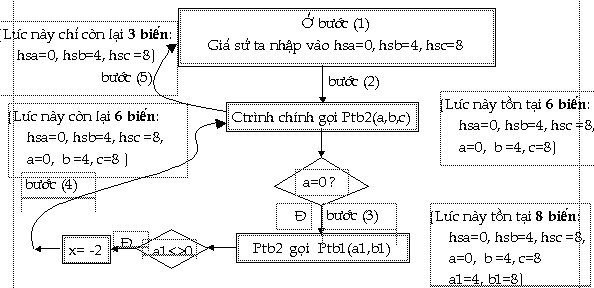
Ở ví dụ trên, thì thủ tục Ptb2 và
thủ tục Ptb1 được gọi là
thủ tục lồng nhau.
Ở dòng (4), ta thấy hsa, hsb, hsc lại
được hiểu là các tham số thực,
chúng truyền giá trị biến cho các tham số
hình thức a, b,
c tương ứng trong thủ tục Ptb2.
Nếu ta lại xét đến thủ
tục con của thủ tục Ptb2 là Ptb1 thì các
tham số a, b, c này (chính xác là b và c) lại là
tham số thực đối với Ptb1, với b
và c được truyền tương ứng
cho các tham số hình thức
a, b của thủ tục Ptb1.
Như vậy ta nhận thấy rằng,
vấn đề xác định được
đâu là biến toàn cục, đâu là biến
cục bộ, đâu là tham số thực và
đâu là tham số hình thức (tham số
biến và tham số trị) là ứng bước
nào mà chương trình đang thực hiện?
Ðây là phần then chốt để nắm
được cách vận hành và kết quả
của chương trình xử lý.
Sơ đồ minh họa cách vận hành và
quản lý biến của chương trình: Hàm
là một chương trình con cho ta 1 giá trị
kiểu vô hướng. Hàm tương tự như
thủ tục nhưng trả về một giá
trị thông qua tên hàm và lời gọi hàm tham gia
trong biểu thức. Cấu trúc một hàm tự đặt gồm:
FUNCTION <Tên hàm> (<Tham số hình
thức : kiểu biến>) : <Kiểu kết
quả> ;
{ các khai báo hằng, biến, kiểu
cụcbbộ... }
BEGIN
{ ... các khai báo trong nội bộ hàm ... }
END ; Trong
đó: -
Tên hàm là tên tự đặt cần tuân
thủ theo nguyên tắc đặt tên trong Pascal. -
Kiểu kết quả là một kiểu vô hướng,
biểu diễn kết quả giá trị của hàm. -
Một hàm có thể có 1 hay nhiều tham
số hình thức, khi có nhiều tham số hình
thức cùng một kiểu giá trị thì ta có
thể viết chúng cách nhau bằng dấu
phẩy (,). Trường hợp các tham số hình
thức khác kiểu thì ta viết chúng cách nhau
bằng dấu chấm phẩy (;). -
Trong hàm có thể sử dụng các hằng,
kiểu, biến đã được khai báo trong
chương trình chính nhưng ta có thể khai báo
thêm các hằng, kiểu, biến dùng riêng trong
nội bộ hàm. Chú ý là phải có một
biến trung gian có cùng kiểu kết quả
của hàm để lưu kết quả của
hàm trong quá trình tính toán để cuối cùng ta
có 1 lệnh gán giá trị của biến trung gian
cho tên hàm. Ví
dụ 7.4:
FUNCTION
TINH (x, y : integer ; z : real ) : real ; Ðây
là một hàm số có tên là TINH với 3 tham
số hình thức x, y, z. Kiểu của x và y là
kiểu số nguyên integer còn kiểu của z là
kiểu số thực real. Hàm TINH sẽ cho
kết quả kiểu số thực real. Ví
dụ 7.5:
Bài toán tính giai thừa (factorials) PROGRAM
giaithua ; VAR
x :
integer ;
FUNCTION factorial (n : integer) : integer ;
VAR heso,
tichso : integer ;
BEGIN
tichso := 1 ;
IF n <= 1 THEN
factorial := 1
ELSE BEGIN
FOR heso
:= 2 TO n DO
tichso := tichso
* heso ;
factorial := tichso;
END ;
END ; BEGIN
Write (' Nhập vào một số nguyên dương
x = '); Readln (x) ;
Writeln (' Với x =
, x , thì giai thừa sẽ là :
x ! = ' ,
factorial(x))
Readln; END.
Ghi
chú : Khi
khai báo kiểu dữ kiệu cho các tham số hình
thức trong thủ tục và hàm, ta cần
phải chú ý điểm sau:
Nếu kiểu dữ liệu của các tham
số hình thức là các kiểu dữ liệu có
cấu trúc (kiểu array, string, kiểu record,... )
thì việc khai báo kiểu dữ liệu cho các
tham số hình thức nên được
khai báo theo cách gián tiếp, tức là
phải thông qua từ khóa TYPE. Ví
dụ 7.6:
Procedure Xuat1(hoten
: string[25]);
Procedure Xuat2(mang:
array[1..10] of integer);
Hai chương trình con Xuat1 và Xuat2 đều
bị lỗi ở phần khai báo kiểu dữ
liệu cho hai tham
số hình thức là hoten và mang.
Ðể khắc phục lỗi này, ta sẽ
khai báo gián tiếp một kiểu dữ liệu
str25 và M10 thông qua từ khóa TYPE như sau: TYPE
Str25=string[25]; {Str25 là một kiểu chuỗi
có độ dài 25}
M10=Array[1..10] of integer; {M10 là một kiểu
dữ kiệu mảng có 10 phần tử nguyên} Tiếp
đến, dùng 2 kiểu dữ liệu mới
định nghĩa Str25 và M10 để định
kiểu cho các tham số hình thức hoten và mang như
sau:
Procedure Xuat1(hoten
: Str25);
Procedure Xuat2(mang:
M10);
Khi
truyền tham số trong Pascal, đòi hỏi
phải có sự tương ứng về tên
của kiểu dữ liệu của các tham
số hình thức và tham số thực. Một
số định nghĩa và qui tắc về
truyền tham số trong Pascal: -
Những tham số hình thức nằm sau từ khóa
VAR gọi là tham số biến (variable parameter).
Với tham số biến, các tham số thực
bắt buộc phải là biến chứ không
được là giá trị. Khi giá trị
của tham số biến thay đổi thì nó
sẽ làm thay đổi giá trị của tham
số thực tương ứng và khi ra khỏi
chương trình con
đó, tham số thực vẫn giữ
giá trị đã được thay đổi
đó. -
Những tham số hình thức không đứng
sau từ khóa VAR gọi là tham số trị (value
parameter), khi đó các tham số thực có thể
là một biến, một biểu thức, một
hằng, hoặc một giá trị số. Các tham
số trị nhận giá trị từ tham số
thực khi truyền như là giá trị ban đầu,
khi giá trị của tham số trị thay đổi
thì nó sẽ không làm thay đổi giá trị
của tham số thực, nghĩa là giá trị
của tham số thực sau khi thoát khỏi chương
trình con vẫn luôn bằng với giá trị
của tham số thực trước khi truyền
đến chương trình con đó.
Do vậy một tham trị không bao giờ là
kết quả tính toán của chương trình
con. Một
vài thí dụ về tham số biến: Ví
dụ 7.7: Viết
chương trình tính lập phương. PROGRAM
Parameter1;
VAR num:
integer; {num
là biến toàn cục}
PROCEDURE LapPhuong(var a:integer);
{a là một tham số biến}
Begin
a:=a*a*a;
End;
Begin
write('Nhập số cần tính lập phương
num = ');
readln(num);
LapPhuong(num); {tham
số thực num được truyền cho tham
số biến a}
writeln('Lập phương của số
vừa nhập =' , num);
readln;
End. Ví
dụ 7.8: PROGRAM
parameter2; VAR
a, b :
integer ;
{biến toàn cục }
PROCEDURE
thamso (x :
integer ; VAR y : integer ) ;
BEGIN
{ x: là tham số trị , còn y là tham
số biến}
x := x + 1 ;
y := y + 1 ;
Writeln (‘Trong procedure thamso, ... ‘) ;
Writeln (' Hai số của bạn là a = , x : 3,
và b = , y : 3 ) ;
END ; BEGIN
Write (' Nhập vào 2 trị số nguyên a, b :
') ; Readln
(a, b) ;
Writeln (' Ban đầu, Bạn đã nhập
vào a =' , a : 3, 'và b =' , b : 3 ) ;
thamso (a, b) ;
{tham số thực a truyền cho tham số
trị x
tham số thực b truyền cho tham số
biến y }
Writeln (' Ngoài procedure thamso, ... ');
Writeln (' Hiện nay, số a là , a : 3, và b là
, b : 3 ') ;
Writeln (' Ta thấy, a không đổi và b thay
đổi ! ') ;
Readln; END. Một
chương trình con mà trong quá trình thiết
lập, nó sẽ gọi chính bản thân nó thì chương
trình con có tính đệ qui (recursion). Ví
dụ 7.9:
Bài toán tính giai thừa (factorials) theo cách
đệ qui. Bài toán này có phần chương
trình chính giống như đã có ở ví dụ
trước: PROGRAM
Giaithua ;
(*Tính giai thừa của số n theo phương
pháp đệ qui *)
VAR x
: integer ;
FUNCTION factorial (n : integer) : longint ;
BEGIN
IF n <= 1 THEN
factorial := 1 {điều
kiện neo}
ELSE factorial
:= n * factorial (n -1);
END ;
BEGIN
Write (' Nhập vào một số nguyên dương
x = ');
Readln (x) ;
Writeln ;
Writeln (' Kết quả ',x,'! =
, factorial(x));
Readln;
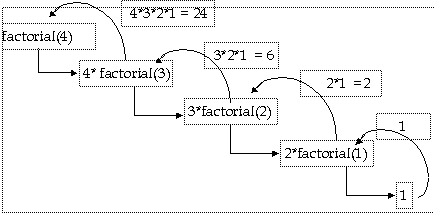
END. Giả sử ta nhập x = 4, thì 4! = factorial(n), với n = 4, ta có sơ đồ minh họa như sau:
Chú
ý: -
Ưu điểm của thuật toán đệ
qui là ngắn gọn. Nó có khả năng định
nghĩa một tập hợp rất lớn các
đối tượng bằng một số các câu
lệnh hữu hạn. Thuật toán đệ qui
có vẻ thích hợp cho các bài toán mà tự thân
cấu trúc dữ liệu của nó đã
được định nghĩa theo lối
đệ qui. -
Có một số thuật toán đệ qui sử
dụng cho các bài toán đơn giản có
thể được thay thế bằng một
thuật toán khác không tự gọi chúng, sự
thay thế đó được gọi là khử
đệ qui. -
Trong một số bài toán ta có thể giải theo
2 cách: thuật toán lặp (xem chương trước)
và thuật toán đệ qui. Thông thường, cách
giải theo thuật toán lặp (WHILE .. DO) thì
tốt hơn so với thuật toán đệ qui
vì đệ qui đòi hỏi thêm bộ nhớ và
thời gian. Khi đó các thanh ghi được
sử dụng cho lưu trữ và khi quay trở
về phải khôi phục lại trạng thái cũ
trong mỗi lần gọi đến chương
trình con. Mức độ phức tạp có
thể gia tăng khi trong chương trình con theo
thuật toán đệ qui có chứa những chương
trình con khác. Vì vậy, khi dùng đệ qui ta
cần thận trọng, nhất là thuật toán này
thường không cho ta thấy rõ trực tiếp
toàn bộ quá trình giải các bước. Nói
chung, chỉ khi naò không thể dùng thuật toán
lặp ta mới nên sử dụng thuật toán
đệ qui. Lập
trình một bài toán lớn rất phức tạp
và vất vả nếu nó phải sử dụng
nhiều thuật toán lập đi lập lại.
Việc tạo ra nhiều mẫu chương trình
con nhằm giảm nhẹ công việc của
một lập trình viên (programmer). Tuy nhiên, mỗi
chương trình con chỉ có ứng dụng
được trong chính chương trình chứa
nó mà thôi. Ðể khỏi mất thời gian để
viết lại chúng, người ta biến
mỗi chương trình con thành các module độc
lập, được biên dịch sẵn và lưu
trữ trên đĩa như một thư
viện. Khi cần ta cứ việc gọi các
module này ra mà không cần phải viết lại
chúng. Mỗi module như vậy được
gọi là một đơn vị chương trình,
hay gọi tắt là UNIT.
Khái niệm Unit đã được vào
sử dụng từ chương trình Pascal version
4.0 trở đi. Có hai loại Unit là các Unit
chuẩn do Turbo Pascal tạo sẵn và các Unit
tự tạo do người lập trình tự
viết ra. a.
Một số Unit chuẩn trong Turbo Pascal 5.5 trở
đi *
Unit SYSTEM
: gồm các hằng, biến, kiểu, hàm,
thủ tục trong version 3.0 *
Unit CRT
: gồm các hằng, biến, kiểu, hàm,
thủ tục liên quan đến *
Unit PRINTER
: gồm các hằng, biến, kiểu, hàm,
thủ tục liên quan đến *
Unit GRAPH
: gồm các hằng, biến, kiểu, hàm,
thủ tục liên quan đến *
Unit TURBO3
: gồm các hằng, biến, kiểu, hàm,
thủ tục liên quan đến *
Unit GRAPH3
: gồm các hằng, biến, kiểu, hàm,
thủ tục liên quan đến *
Unit DOS
: gồm các hằng, biến, kiểu, hàm,
thủ tục liên quan đến hệ
điều
hành MS-DOS *
Unit OVERLAY
: gồm các hằng, biến, kiểu, hàm,
thủ tục liên quan đến
Các Unit trên được lưu trữ trong
tập tin TURBO.TPL của Turbo Pascal.
Chúng ta có thể sử dụng chương
trình TPUMOVER.EXE để lấy ra hoặc
đưa vào một hay nhiều Unit nhằm
tiết kiệm bộ nhớ hay tăng cường
tiện ích sử dụng. Muốn
sử dụng UNIT thì trong đầu chương
trình ta phải khai báo Unit theo cú pháp sau: Ví
dụ 7.10
USES CRT, GRAPH
; Ðặc
biệt, chỉ riêng Unit SYSTEM thì không cần
phải khai báo. *
ClrScr
: thủ tục xóa màn hình *
ClrEol
: thủ tục xóa ký tự bên phải con
trỏ màn hình, sau khi xóa con trỏ
vẫn
ở tại chỗ *
InsLine
: thủ tục xen vào một hàng ở
vị trí con trỏ màn hình *
DelLine
: thủ tục xóa bỏ một hàng ở
vị trí con trỏ màn hình *
GotoXY(XPos, Ypos): đưa con trỏ màn hình về
vị trí có tọa độ Xpos và *
Delay(time): tạo thời gian trễ tính theo
milisecond. Time là một số nguyên *
Sound(F)
: thủ
tục tạo ra âm thanh với tần số F
(hz). F là số nguyên *
NoSound
: thủ
tục tắt âm thanh *
LowVideo và NormVideo: thủ tục màn hình, khi
gọi LowVideo thì mọi ký *
TextBackGround (color): thủ
tục chọn màu nền, color
cho ở bảng (từ 1 -7) *
KeyPressed: hàm
cho giá trị kiểu kết quả Boolean, cho giá
trị là True
nếu có một phím được bấm. *
TextColor (color): thủ
tục chọn màu chữ, color lấy ở
bảng
Các
hằng số màu của CRT unit
Ðể tạo ra màu nhấp nháy, ta cộng
thêm hằng số Blink của CRT vào bất
kỳ màu chữ mà ta chọn. Ta không thể làm
nhấp nháy màu nền. Ví
dụ để trình bày chữ vàng trên nền
xanh, ta viết:
TextColor(Yellow) ;
TextBackground(Blue) ; Muốn
có một dòng chữ đỏ nhấp nháy thì ra
lệnh:
TextColor(Red + Blink) ; *
ReadKey
: hàm có
kiểu kết quả là Char, khi nhấn các phím
chức năng
trên bàn phím thì có kết quả là 1 ký tự mã
ASCII. Nếu ký tự đầu tiên do ReadKey
trả về bằng ASCII 0 thì ký tự kế
theo sẽ chỉ định phím như ở
bảng dưới. Các phím Home, phím mũi tên,
... luôn tạo nên một ký tự đi theo ASCII
0. Các phím chức năng từ F1 đến F10
sinh ra một trong 4 ký tự tùy theo ta dùng với
tổ hợp phím Alt, Ctrl hay Shift hay dùng một mình.
Các phím
chức năng đặc biệt
Ðể tạo ra một Unit của mình cần đi qua các bước sau: Bước
1 :
Tạo ra một file Unit có phần mở
rộng là .PAS với bố cục sau: UNIT
<Tên Unit> ;
(* Chú ý : Tên Unit phải trùng với tên File
*) INTERFACE
(* Chú ý : Phần giao diện với bên ngoài,
không có dấu ; ở đây *)
[Uses <danh sách các unit>];
{Khai báo các unit dùng trong chương trình }
[Khai báo các hằng, kiểu, biến dùng
chung] ;
[Khai báo các thủ tục, hàm (tên, danh sách
tham số của thủ tục và hàm] ; IMPLEMENTATION
(* Cài đặt các hàm, thủ tục
của Unit, không có dấu ; ở đây *)
[Các khai báo kiểu, hằng, biến cục
bộ ];
[Nội dung cài đặt các thủ tục,
hàm của unit ]; [BEGIN]
(* Phần khởi tạo : Initialization Part *)
[Các lệnh khởi tạo ]; END.
(* Dù có BEGIN để khởi tạo hay không,
ở đây vẫn có END. *) Bước
2 :
Dịch file này lên đĩa theo trình tự
sau: i).
Gõ Alt - C để
vào Menu COMPILE ii).
Ði đến mục Destination và nhấn Enter
để chương trình tự động
đổi Memory thành
Disk iii).
Gõ C (hoặc F9) để biên dịch chương
trình tạo nên một file
.TPU iv).
Khi dịch xong gõ một phím bất kỳ.
Sau đó ta có thể lập lại bước a
và b Ví
dụ 7.11:
Tạo một UNIT tính Cộng, Trừ, Nhân,
Chia cho học sinh tiểu học.
Tên file Unit là TTIEUHOC.PAS với nội dung sau: UNIT
TTieuHoc ;
{Phần đầu : Chương trình Toán
Tiểu học } INTERFACE
{Phần giao diện}
PROCEDURE Cong (Var So1, So2, So3 : Real) ;
PROCEDURE Tru
(Var So1, So2, So3 : Real) ;
PROCEDURE Nhan (Var So1, So2, So3 : Real) ;
PROCEDURE Chia (Var
So1, So2, So3 : Real) ; INPLEMENTATION
{Phần cài đặt }
PROCEDURE Cong ;
BEGIN
IF So1 + So2 = So3 THEN Writeln ('Giỏi lắm ! Em
đã làm đúng! ')
ELSE Writeln (' Rất tiếc, em đã làm sai !
');
END;
PROCEDURE Tru ;
BEGIN
IF So1 - So2 = So3 THEN Writeln (' Giỏi lắm ! Em
đã làm đúng!')
ELSE Writeln (' Rất tiếc, em đã làm sai !
');
END;
PROCEDURE Nhan ;
BEGIN
IF So1 * So2 = So3 THEN Writeln ('Giỏi lắm ! Em
đã làm đúng !')
ELSE Writeln (' Rất tiếc, em đã làm sai !
');
END;
PROCEDURE Chia ;
BEGIN
IF So2 = 0 THEN Writeln ('Số chia phải khác 0')
ELSE
IF So1 / So2 = So3 THEN Writeln ('Giỏi lắm! Em
đã làm đúng! ')
ELSE Writeln (' Rất tiếc, em đã làm sai !
');
END; END.
{Chấm dứt UNIT } Sau
khi gõ chương trình Unit trên, đổi Compile
Destination thành Disk, biên dịch và tạo tập
tin TTIEUHOC.TPU trên đĩa. Chương
trình Pascal cho bài toán Cộng, trừ, Nhân, Chia dùng
Unit TTIEUHOC: PROGRAM
Toan_Tieu_Hoc ; USES
CRT, TTieuHoc ; VAR
chon : Integer ;
So1, So2, So3 : Real ;
PROCEDURE
Menu (Var chon : integer) ;
BEGIN
ClrScr ;
Writeln (' == TOÁN TIỂU HỌC == ') ;
Writeln (' =
0. Chấm
dứt
= ') ;
Writeln (' = 1.
Toán cộng
= ') ;
Writeln (' =
2. Toán
trừ
= ') ;
Writeln (' =
3. Toán
nhân
= ') ;
Writeln (' =
4. Toán
chia
= ') ;
Writeln (‘ ================== ‘) ;
Write
(' Bạn chọn số mấy ?
') ;
Readln (chon);
END ;
PROCEDURE nhapso
(Var So1, So2, So3 : real );
BEGIN
Write (' Nhập vào số thứ 1 :
') ; Readln(So1)
;
Write (' Nhập vào số thứ 2 :
') ; Readln(So2)
;
Write (' Kết quả là
: ')
; Readln (So3) ;
END ; {=====================Chương
Trình Chính ========================}
BEGIN
CLRSCR;
REPEAT
Menu (chon) ;
CASE chon OF
1 : BEGIN
Writeln ;
Writeln (' == Toán
cộng == ') ;
Nhapso(So1, So2, So3) ;
Cong(So1, So2, So3) ;
END;
2 : BEGIN
Writeln ;
Writeln (' == Toán
trừ == ') ;
Nhapso(So1, So2, So3) ;
Tru(So1, So2, So3) ;
END;
3 : BEGIN
Writeln ;
Writeln (‘ == Toán
nhân == ‘) ;
Nhapso(So1, So2, So3) ;
Nhan(So1, So2, So3) ;
END;
4 : BEGIN
Writeln ;
Writeln (‘ == Toán
chia == ‘) ;
Nhapso(So1, So2, So3) ;
Chia(So1, So2, So3) ;
END;
END; {case}
Writeln (' Gõ bất kỳ phím nào để
tiếp tục ... ');
Readln;
UNTIL chon = 0;
END.
{Ngưng làm toán} =============================================================== TOP
- DOWN STRUCTURED PROGRAMMING hay LẬP
TRÌNH THEO CẤU TRÚC TRÊN - XUỐNG ---
oOo --- Nếu
các bạn là một người mới bắt
đầu khởi sự thực hành lập trình
một bài toán nào đó, các bạn sẽ thường
tự hỏi: Ta phải bắt đầu
bằng việc gì đây? Ðây là một câu
hỏi không phải ai cũng trả lời chung
được. Tuy nhiên, dựa vào kinh nghiệm
thu thập được của những người
lập trình tài tử và của những lập
trình viên chuyên nghiệp, tác giả Francis Scheid,
trong tác phẩm Computer and Programming của mình,
đã cho một số lời khuyên sau : 1.
Ôn lại những kinh nghiệm đã qua để
xem coi vấn đề của bạn có chút gì tương
tự đến các vấn đề mà bạn
đã từng chạm trán trước đây không; 2.
Trước tiên, thử làm một phiên
bản đơn giản. Nếu có thể,
đưa ngay vào một số trường
hợp đặc biệt mà bạn
có, nhằm tạo chương trình bạn có
một vẻ gì sâu sắc. 3.
Chia bài toán ra thành những bài nhỏ,
rồi tiếp tục chẻ những bài nhỏ
này thành những phần nhỏ hơn, nếu
được, chẻ tiếp những phần
nhỏ này thành những mảnh nhỏ hơn
nữa, sau đó giải quyế từng phần
hay mảnh nhỏ này.
Mỗi thuật toán có thể thể
hiện bằng lưu đồ (flow chart). Lưu
đồ chính là bản đồ lộ trình
của thuật toán. Không hẳn tất cả
những chuyên viên máy tính phải thực
hiện lưu đồ trước khi lập trình
nhưng nhờ có lưu đồ mà công việc
của bạn trở nên rõ ràng và mang tính logic hơn.
Bạn sẽ không cảm thấy bối rối
khi cần phải trình bày tiến trình giải toán
của bạn cho người khác hiểu. Bạn
có thể mất một ít thời gian cho lưu
đồ nhưng nó có giá trị hơn cả ngàn
từ nếu phải cắt nghĩa thuật toán.
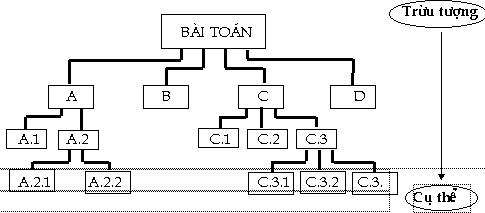
Chúng ta hãy tưởng tượng bài toán
to lớn của chúng ta như một cây cổ
thụ nhiều cành lá rậm rạp. Ta muốn
đốn cây này về nhà làm củi chụm và
dĩ nhiên, ta không thể nào chặt ngang gốc
cây mà vác về nhà (thí dụ này không có ý
khuyến khích phá hoại môi trường đâu
nhé ! ). Vậy tại sao ta không tỉa từng cành
nhỏ rồi dần dần thanh toán luôn cả cây
? Giải quyết vấn đề của chúng ta
cũng vậy. Bạn cứ xem bài toán của chúng
ta như một gốc cây lộn ngược
đầu. Chia nhỏ bài toán ra thành những
vấn đề nhỏ hơn, rồi nhỏ hơn
nữa nếu nó còn phức tạp, như minh
họa ở hình sau đây:
Trong hình vẽ trên, bài toán được
phân thành 4 vấn đề nhỏ hơn là A, B,
C và D. Vấn đề B và D có thể giải
quyết được ngay. Riêng vấn đề
A và C thì lại tiếp tục chia nhỏ hơn
nữa để thành những mảnh nhỏ có
thể giải quyết được. Ở
đây các nhánh cây không dài ngắn như nhau,
dễ hiểu bởi vì mức độ phức
tạp của mỗi vấn đề không
thể như nhau và tùy theo thuật toán cần
giải quyết mà ta phân nhỏ nó ra. Bài toán
của chúng ta sẽ đi từ vấn đề
trừu tượng đến cụ thể. Cách
giải quyết như vậy giống như
hệ thống phân quyền trong tổ chức chính
phủ:
Lập trình cấu trúc là một trường
phái lập trình xuất hiện vào thập niên
1970 và đã nhanh chóng được nhiều người
hưởng ứng. Ðiểm cơ bản trong
lập trình cấu trúc là tổ chức chương
trình thành một hệ phân cấp (hierarchy) và
phải điều khiển sao cho các mối tương
tác giữa các thành phần trong hệ là tối
thiểu. Ðây chính là ý tưởng của
một phép tinh chế từng bước (stepwise
refinement) hay phương pháp chia để trị
trong giải bài toán theo cách top-down. Một khi ta
đã thực hiện việc phân tích top-down xong,
những mảnh bài toán chi tiết nhất sẽ
được giải theo cách của 1 trong 3 thành
phần thuật toán sau : *
Dòng tuần tự (Sequential Flow) : Trong thuật
giải này, các bước giải được
thể hiện ở trong một luồng lệnh
tuần tự như hình vẽ sau:
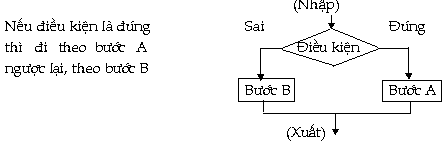
*
Dòng điều kiện (Conditional Flow): Trong
thực tế ở nhiều bài toán máy tính, ta
sẽ đi đến việc chọn lựa
một trong hai điều kiện. Mỗi điều
kiện (Ðúng hoặc Sai) sẽ dẫn đến
một quyết định khác nhau. Minh họa
ở hình sau: *
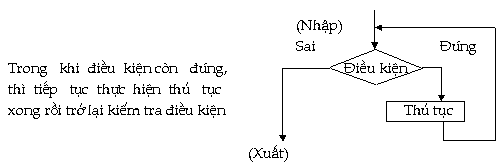
Dòng lặp (Repetitive Flow) :
Trong nhiều trường hợp, ta cần
thực hiện nhiều lần liên tiếp
một hay nhiều thao tác cho để khi một
điều kiện được thỏa.
Cha đẻ của ngôn ngữ lập trình
Pascal là N.Wirth đã phát triển phương pháp
tinh chế từng bước, xem nó như
một phương pháp khoa học cần
thiết cho việc phân tích vấn đề và
lập trình. Khởi đầu, chương trình phải được thể hiện khái quát vấn đề, nêu bậc sự phân tích tổng thể bài toán. Ở từng bước kế tiếp sau đó, sẽ có các giải pháp giải quyết vấn đề một cách chi tiết hơn, mỗi giải pháp như vậy là một sự đặc tả (specification) công việc. Như vậy, từng bước một, ta dần dần tinh chế bài toán. Sự tinh chế này phải hướng đến các thuật toán của ngôn ngữ lập trình. Nếu các bài toán nhỏ trở nên đơn giản thì ta thay nó bằng các câu lệnh. Nếu nó tỏ ra còn phức tạp thì ta xem đó như một thủ tục và tiếp tục tìm cách tinh chế nó. Trong quá trình tinh chế, cần thiết đưa ra những cách biểu diễn dữ liệu đi song song với cách chi tiết hoá việc giải quyết bài toán. Ðây là một phương pháp khoa học nhưng cũng mang một phần tính nghệ thuật thể hiện sự nhạy bén trong tư duy của người lập trình.
|