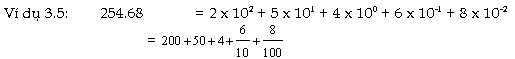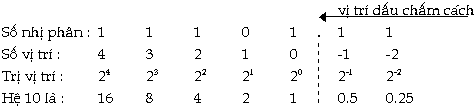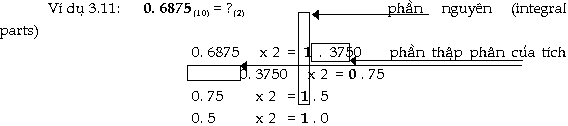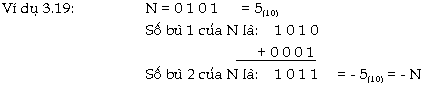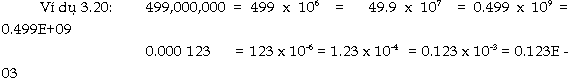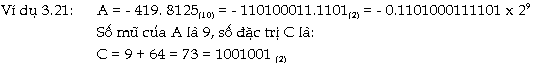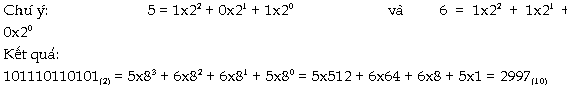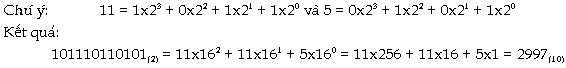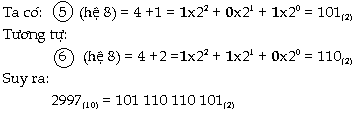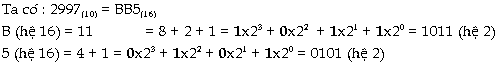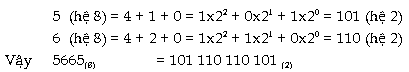|
BÀI ÐỌC THÊM CHUYỂN ÐỔI HỆ THỐNG SỐ DỰA TRÊN HỆ 8 VÀ HỆ 16.
Hệ
đếm là tập hợp các ký hiệu và qui
tắc sử dụng tập ký hiệu đó
để biểu diễn và xác định các giá
trị các số. Mỗi hệ đếm có
một số ký số (digits) hữu hạn.
Tổng số ký số của mỗi hệ đếm
được gọi là cơ số (base hay
radix), ký hiệu là b. Hệ
đếm phổ biến hiện nay là hệ
đếm La mã và hệ đếm thập phân. a.
Hệ đếm La mã
Hệ đếm La mã được xem như là
hệ đếm có hệ thống đầu tiên
của con người. Hệ đếm La mã
sử dụng các ký hiệu ứng với các giá
trị như sau: I
= 1 V = 5
X = 10 L = 50
C = 100 D = 500
M = 1000 Ký
số La mã có một số qui tắc sau: ·
Số
lần n liên tiếp
kế nhau của mỗi ký hiệu thể
hiện giá trị ký hiệu tăng lên n lần.
Số lần n
chỉ là là 1 hoặc 2 hoặc 3. Riêng ký hiệu
M được phép xuất hiện 4 lần liên
tiếp. Ví
dụ 3.1:
III = 3 x 1 = 3;
XX = 2 x 10 = 20;
MMMM = 4000, ... ·
Hai
ký hiệu đứng cạnh nhau, nếu ký
hiệu nhỏ hơn đứng trước thì
giá trị của chúng sẽ là hiệu số
của giá trị ký hiệu lớn trừ giá
trị ký hiệu nhỏ hơn. Ví
dụ 3.2:
IV = 5 -1 = 4;
IX = 10 - 1 = 9;
CD = 500 - 100 = 400;
CM = 1000 - 100 = 900 ·
Hai
ký hiệu đứng cạnh nhau, nếu ký
hiệu nhỏ đứng sau thì giá trị
của chúng sẽ là tổng số của 2 giá
trị ký hiệu. Ví
dụ 3.3: XI = 10 + 1 = 11;
DCC = 500 + 100 + 100 = 700
Giá trị 3986 được thể hiện là:
MMMCMLXXXVI ·
Hệ
đếm La mã hiện ít được sử
dụng trong tính toán hiện nay.
b.
Hệ đếm thập phân (decimal system) Hệ
đếm thập phân hay hệ đếm cơ
số 10 là một trong các phát minh của người
Ả rập cổ, bao gồm 10 ký số theo ký
hiệu sau: 0,
1, 2, 3, 4, 5, 6, 7, 8,
9
Qui
tắc tính giá trị của hệ đếm này
là mỗi đơn vị ở một hàng
bất kỳ có giá trị bằng 10 đơn
vị của hàng kế cận bên phải. Ở
đây b = 10. Bất kỳ số nguyên dương
trong hệ thập phân có thể thể hiện
như là một tổng các chuỗi các ký số
thập phân nhân cho 10 lũy thừa, trong đó
số mũ lũy thừa được tăng
thêm 1 đơn vị kể từ số mũ lũy
thừa phía bên phải nó. Số mũ lũy
thừa của hàng đơn vị trong hệ
thập phân là 0. Ví
dụ 3.4: Số 5246 có
thể được thể hiện như sau: 5246
= 5 x 103 + 2 x 102 + 4 x 101 + 6 x
100 =
5 x 1000 + 2 x 100 + 4 x 10 + 6 x 1
Thể
hiện như trên gọi là ký hiệu mở
rộng của số nguyên. Vì
5246 = 5000 + 200 + 40 + 6
Như
vậy, trong số 5246 : ký số 6 trong số nguyên
đại diện cho giá trị 6 đơn
vị (1s), ký số 4 đại diện cho giá
trị 4 chục (10s), ký số 2 đại
diện cho giá trị 2 trăm (100s) và ký số 5
đại diện cho giá trị 5 ngàn (1000s). Nghĩa
là, số lũy thừa của 10 tăng dần 1
đơn vị từ trái sang phải tương
ứng với vị trí ký hiệu số,
100
= 1
101 = 10
102 = 100
103 = 1000
104 = 10000 ...
Mỗi
ký số ở thứ tự khác nhau trong số
sẽ có giá trị khác nhau, ta gọi là giá
trị vị trí (place value).
Phần phân số trong hệ thập phân sau dấu chấm phân cách (theo qui ước của Mỹî) thể hiện trong ký hiệu mở rộng bởi 10 lũy thừa âm tính từ phải sang trái kể từ dấu chấm phân cách:
Tổng
quát, hệ đếm cơ số b ( ·
Có
b ký số để thể hiện giá trị
số. Ký số nhỏ nhất là 0 và lớn
nhất là b-1. ·
Giá
trị vị trí thứ n trong một số
của hệ đếm bằng cơ số b lũy
thừa n : Số
N(b) trong hệ đếm cơ số (b) thể
hiện : trong
đó, số N(b) có n+1 ký số chẵn ở
phần nguyên và m ký số lẻ, sẽ có giá
trị là :
c.
Hệ đếm nhị phân (binary number
system) Với
b = 2, chúng ta có hệ đếm nhị phân. Ðây
là hệ đếm đơn giản nhất
với 2 chữ số là 0 và 1. Mỗi chữ
số nhị phân gọi là BIT (viết tắt
từ chữ BInary digiT). Hệ nhị phân tương
ứng với 2 trạng thái của các linh
kiện điện tử trong máy tính chỉ có:
đóng (có điện) ký hiệu là 1 và tắt
(không điện) ký hiệu là 0. Vì hệ
nhị phân chỉ có 2 trị số là 0 và 1, nên
khi muốn diễn tả một số lớn hơn,
hoặc các ký tự phức tạp hơn thì
cần kết hợp nhiều bit với nhau.
Ta
có thể chuyển đổi hệ nhị phân
theo hệ thập phân quen thuộc. Ví
dụ 3.6: Số
như
vậy: 11101.11(2)
= 1x16 + 1x8
+ 1x4 + 0x2
+ 1x1 + 1x0.5
+ 1x0.25
= 29.75
(10)
tương
tự số 10101
(hệ 2) sang hệ thập phân sẽ là: 10101(2)
= 1x24 + 0x23
+ 1x22 + 0x21
+ 1x20 = 8 +
0 + 4 + 0 + 1 = 13(10)
d.
Hệ đếm bát phân (octal number system) Nếu dùng 1 tập hợp 3 bit thì có thể biểu diễn 8 trị khác nhau : 000, 001, 010, 011, 100, 101, 110, 111. Các trị này tương đương với 8 trị trong hệ thập phân là 0, 1, 2, 3, 4, 5, 6, 7. Tập hợp các chữ số này gọi là hệ bát phân, là hệ đếm với b = 8 = 23. Trong hệ bát phân, trị vị trí là lũy thừa của 8.
e.
Hệ đếm thập lục phân
(hexa-decimal number system) Hệ
đếm thập lục phân là hệ cơ
số Ví
dụ 3.8:
Ghi
chú: Một số chương trình qui định
viết số hexa phải có chữ H ở
cuối chữ số. Ví
dụ 3.9: Số 15
viết là FH.
Bảng
qui đổi tương đương 16 chữ
số đầu tiên của 4 hệ đếm
Tổng
quát: Lấy số
nguyên thập phân N(10) lần lượt chia cho b
cho đến khi thương số
bằng 0. Kết quả số chuyển đổi
N(b) là các dư số trong phép chia viết ra theo
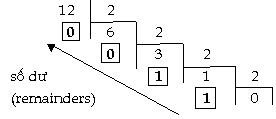
thứ tự ngược lại. Ví
dụ 3.10: Dùng
các phép chia 2 liên tiếp, ta có một loạt các
số dư như sau:
Kết
quả: g.
Ðổi phần thập phân từ hệ thập
phân sang hệ cơ số b Tổng
quát: Lấy số
nguyên thập phân N(10) lần lượt nhân cho b
cho đến khi phần thập
phân của tích số bằng 0. Kết quả
số chuyển đổi N(b) là các số
phần nguyên trong phép nhân viết ra theo thứ
tự tính toán.
Kết
quả: Trong
số học nhị phân chúng ta cũng có 4 phép
toán cơ bản như trong số học thập
phân là cộng, trừ, nhân và chia. Qui tắc
của 2 phép tính cơ bản cộng và nhân:
Ghi chú: Với phép cộng trong hệ nhị phân,
1 + 1 = 10, số 10 (đọc là một - không) chính
là số 2 tương đương trong hệ
thập phân. Viết 10 có thể hiểu là
viết 0 nhớ 1. Một cách tổng quát, khi
cộng 2 hay nhiều chữ số nếu giá
trị tổng lớn hơn cơ số b thì
ta viết phần lẻ và nhớ phần lớn
hơn sang bên trái cạnh nó. Ví
dụ 3.12: Cộng 2
số 0101 + 1100 = ?
Ví
dụ 3.13: Nhân 2
số 0110 x 1011 = ?
Phép
trừ và phép chia là các phép toán đặc
biệt của phép cộng và phép nhân. Ví
dụ 3.14:
Trừ hai số
Ví
dụ 3.15:
Chia hai số
Qui
tắc 1: Khi nhân một số nhị phân với Ví
dụ 3.16:
Qui
tắc 2: Khi chia một số nguyên nhị phân cho
Ví
dụ 3.17:
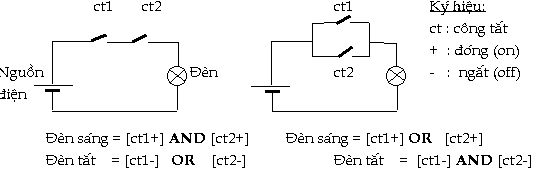
Mệnh
đề logic là mệnh đề chỉ
nhận một trong 2 giá trị : Ðúng (TRUE)
hoặc Sai (FALSE), tương đương
với TRUE = 1 và FALSE = 0.
Qui
tắc:
TRUE = NOT FALSE
và
FALSE = NOT TRUE Phép
toán logic áp dụng cho 2 giá trị TRUE và FALSE
ứng với tổ hợp AND (và) và OR (hoặc)
như sau:
Dữ
liệu số trong máy tính gồm có số nguyên
và số thực.
Số
nguyên gồm số nguyên không dấu và số
nguyên có dấu. *
Số
nguyên không dấu là số không có bit dấu như
1 byte = 8 bit, có thể biểu diễn *
Số
nguyên có dấu thể hiện trong máy tính ở
dạng nhị phân là số dùng 1 bit làm
bít dấu, người ta qui ước dùng bit
ở hàng đầu tiên bên trái làm bit dấu
(S): 0 là số dương và 1 cho số âm. Ðơn
vị chiều dài để chứa thay đổi
từ 2 đến 4 bytes.
Ta
thấy, với chiều dài 16 bit : bit đầu là
bit dấu và 15 bit sau là bit số Trị
dương lớn nhất của dãy 2 bytes sẽ
là: Trị
âm lớn nhất trong dãy 2 bytes là
Ðể
thể hiện số âm trong hệ nhị phân ta
có 2 khái niệm: -
Số bù 1: Khi đảo ngược tất
cả các bit của dãy số nhị phân: 0 thành
1 và 1 thành 0, dãy số đảo đó gọi là
số bù 1 của số nhị phân đó.
-
Số bù 2: Số bù 2
của số N là số đảo dấu của
nó (-N). Trong hệ nhị phân, số bù 2
được xác định bằng cách lấy
số bù 1 của N rồi cộng thêm 1.
Ðối
với các số thực (real number) là số có
thể có cả phần lẻ hoặc phần
thập phân. Trong máy tính, người ta biễu
diễn số thực với số dấu
chấm tĩnh (fixed point number) và số dấu
chấm động (floating point number).
a.
Số dấu chấm tĩnh: thực chất là
số nguyên (integers) là những số không có
chấm thập phân
b.
Số dấu chấm động: là số có
chữ số phần lẻ không cố định.
Mỗi số như vậy có
thể trữ và xử lý trong máy tính ở
dạng số mũ.
Ghi
chú: Dấu chấm thể hiện trong máy tính
để phân biệt phần lẻ, dấu
phẩy tượng trưng cho phần ngàn,
được viết theo qui ước của
Mỹ.
Tổng
quát, số dấu chấm động được
biểu diễn theo 3 phần :
- phần
dấu S (sign) : 0 cho + và 1 cho - -
phần định trị m (mantissa)
- phần
mũ e (exponent), có thể là số nguyên dương
(+) hoặc âm (-) với
một số X bất kỳ, có thể viết :
X = ±
m . b e = ±
m E e
Trong
đó, b là cơ số qui ước, trị
số mũ e có thể thay đổi tùy theo
số vị trí cần dời dấu chấm
để có lại trị số ban đầu.
Khi dời dấu chấm sang Ðể
biểu diễn số có dấu chấm động,
người ta dùng dãy 32 bit với hệ thống
cơ số 16. Trong đó, 1 bit cho phần dấu,
7 bit cho phần mũ để biểu diễn
phần đặc trị C (characteristic) và 24 bit
cho phần định trị m.
Phần
mũ có 7 bit = C
= số mũ biểu diễn + 64
Trong
máy tính, số A sẽ được trữ theo
vị trí nhớ 32 bit như sau :
Ðể
có thể biễu diễn các ký tự như
chữ cái in và thường, các chữ số, các
ký hiệu... trên máy tính và các phương
tiện trao đổi thông tin khác, người ta
phải lập ra các bộ mã (code system) qui ước
khác nhau dựa vào việc chọn tập hợp
bao nhiêu bit để diễn tả 1 ký tự tương
ứng, ví dụ các hệ mã phổ biến :
-
Hệ
thập phân mã nhị phân BCD (Binary Coded Decima) dùng
6 bit.
-
Hệ
thập phân mã nhị phân mở rộng EBCDIC
(Extended Binary Coded Decimal
Interchange Code) dùng 8 bit tương đương 1
byte để biễu diễn 1 ký tự.
-
Hệ
chuyển đổi thông tin theo mã chuẩn
của Mỹ ASCII (American Standard Code
for Information Interchange) là hệ mã thông dụng
nhất hiện nay trong kỹ thuật tin học.
Hệ mã ASCII dùng nhóm 7 bit hoặc 8 bit để
biểu diễn tối đa 128
hoặc 256 ký tự khác nhau và mã hóa theo ký
tự liên tục theo cơ số 16.
Hệ
mã ASCII 7 bit, mã hoá 128 ký tự liện tục như
sau:
0
:
NUL (ký tự
rỗng) 1
- 31
:
31 ký tự điều khiển 32
- 47
:
các dấu trống SP (space)
! # $ % & ( ) * + , - . / 48
- 57
:
ký số từ 0 đến 9 58
- 64
:
các dấu : ; < = > ? @ 65
- 90
:
các chữ in hoa từ A đến Z 91
- 96
:
các dấu [ \
] _
` 97
- 122
:
các chữ thường từ a đến z 123
- 127
:
các dấu { |
} ~
DEL (xóa) Hệ
mã ASCII 8 bit (ASCII mở rộng) có thêm 128 ký
tự khác ngoài các ký tự nêu trên gồm các
chữ cái có dấu, các hình vẽ, các đường
kẻ khung đơn và khung đôi và một
số ký hiệu đặc biệt (xem phụ
lục). BẢNG
MÃ ASCII với 128 ký tự đầu tiên
PHỤ
LỤC 3.2 BẢNG
MÃ ASCII với ký tự số 128 - số 255
CHUYỂN
ÐỔI HỆ THỐNG SỐ DỰA TRÊN HỆ 8
VÀ HỆ 16 ---
oOo --- Trong
phần bài giảng, chúng ta đã làm quen với
cách chuyển đổi giữa hệ 2 và hệ
10. Tuy nhiên, ở những trị số lớn và
dài thì làm cách trên trở nên rất phức
tạp và dễ nhầm lẫn, ví dụ :
Trong
ví dụ thứ nhất ta phải liên tiếp làm
nhiều phép nhân và ở ví dụ thứ hai, ta
lại thực hiện nhiều phép chia liên
tiếp. Người
ta đưa ra hệ thống số trung gian là
hệ 8 và hệ 16 để giải quyết:
Thông
qua hệ 8 và hệ
16 để chuyển đổi hệ 2 sang
hệ 10 Chia
số nhị phân làm thành từng bộ 3 số
và 4 số liên tiếp theo thứ tự tương
ứng với cách thông qua hệ 8 và hệ 16 và
dùng phương pháp nhân với các thừa
số bên
trên tương ứng rồi cộng lại . Ví
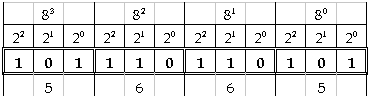
dụ1: THÔNG
QUA HỆ 8: Chia số nhị phân từng bộ 3
số:
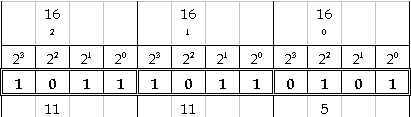
THÔNG
QUA HỆ 16: Chia
số nhị phân thành bộ 4 số
Thông
qua hệ 8 và hệ 16 để chuyển hệ
10 sang hệ 2 Cách
làm tương tự như trên, nhưng thay phép
nhân thành phép chia và lấy các số dư
của phép chia ngược từ dưới lên
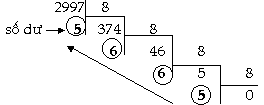
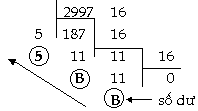
trên để chuyển đổi. Ví
dụ2: THÔNG QUA HỆ 8:
Suy
ra:
Chuyển
hệ 8 sang hệ 16 và ngược lại:
Ta
có thể dùng hệ 10 hoặc hệ 2 làm trung
gian để chuyển đổi hệ 8 sang
hệ 16 và ngược lại. Thông thường
dùng hệ 2 để trung chuyển có thuận
lợi hơn. Ví
dụ 3: Cách
làm như sau: Bước
1: Chuyển hệ 8 thành
hệ 2: biểu thị từng trị số trong
hệ 8 thành từng nhóm 3 số và ghép
các nhóm đó lại.
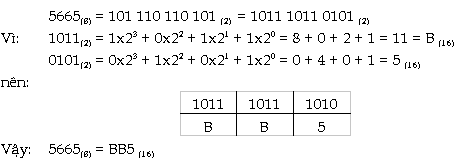
Bước
2: Chia dãy số hệ 2 vừa có được
thành các bộ 4 số và chuyển các bộ
đó sang hệ 16
Việc chuyển từ hệ 16 sang hệ 8 ta cũng tiến hành 2 bước như vậy. |