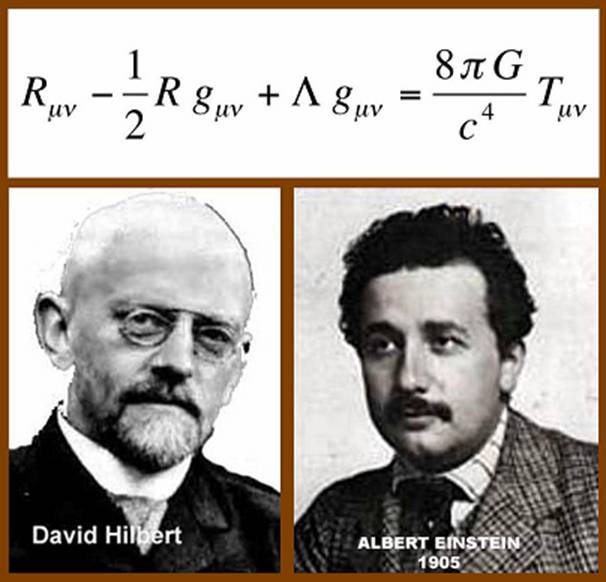Vietsciences ; Phạm Việt Hưng ; Pham Viet Hung; Emmy Noether (1882-1935), người phụ nữ đã giúp Einstein hoàn thiện Thuyết Tương Đối ;science, khoa hoc, khoahoc, tin hoc, informatique;computer; vat ly; physics, physique, chimie, chemistry, hoa hoc, sinh vat, biologie, biology;biochimie;biochemistry;a

Nếu Newton vĩ đại nhờ đã đứng trên vai những người khổng lồ thì Amalie Emmy Noether cũng vô cùng vĩ đại vì bà đã nâng trên đôi vai phụ nữ yếu ớt của mình hai người khổng lồ của thế kỷ 20 – Albert Einstein và David Hilbert!

Ai cũng biết Einstein là một trong những nhà vật lý vĩ đại nhất của mọi thời đại, và Hilbert cũng được coi là một trong những nhà toán học vĩ đại nhất của mọi thời đại, nhưng ít người để ý rằng Emmy Noether là người phụ nữ được tạo hoá sinh ra để giúp đỡ trực tiếp cho David Hilbert và gián tiếp cho Albert Einstein trong việc xây dựng Phương Trình Trường Hấp Dẫn (Field Equation of Gravity) – phương trình cốt lõi làm nên Thuyết Tương Đối Tổng Quát (General Theory of Relativity), một lý thuyết được Einstein công bố vào năm 1916 và đã trở thành một trong hai trụ cột của vật lý hiện đại.

Sự giúp đỡ đó dẫn tới kết quả là cả Einstein lẫn Hilbert cùng rút ra Phương Trình Trường gần như vào cùng một thời điểm, và do đó đã xẩy ra một cuộc tranh chấp vô tiền khoáng hậu giữa hai nhân vật khổng lồ này về quyền tác giả Phương Trình Trường, mãi cho đến cuối thế kỷ 20 mới có câu trả lời dứt khoát, rằng quyền tác giả Phương Trình Trường thuộc về Einstein.

Nhưng Emmy Noether không chỉ quan trọng đối với Einstein và Hilbert, mà còn quan trọng đối với toàn bộ nền vật lý hiện đại, đến nỗi có thể nói rằng nếu không có bà, khoa học sẽ không thể có những hiểu biết sâu sắc về vũ trụ như hiện nay, bởi chính là bà là người thiết lập nên một trong những nền móng quan trọng bậc nhất trong vật lý hiện đại – tư tưởng về tính đối xứng của vũ trụ.

Không phải ngẫn nhiên mà Bách Khoa Toàn Thư Wikipedia nhận định bà là nhà toán học nữ quan trọng nhất trong lịch sử toán học!

Tài năng của bà thực ra có thể xếp ngang hàng với Einstein và Hilbert, nhưng chua chát thay, trong khi Einstein được cả thế giới biết đến như một thiên tài vĩ đại nhất của thế kỷ 20, Hilbert cũng được coi là một trong ba nhân vật định hình cho tư tưởng toán học thế kỷ 20, thì Emmy Noether hầu như chẳng được mấy ai biết đến, trừ những người làm việc trong một chuyên ngành hẹp của toán học và vật lý.

Tại sao vậy? Phải chăng vì những công trình của Noether quá khó để hiểu? Nhưng tại sao người ta có thể hiểu được những lý thuyết cực kỳ khó hiểu của Einstein và Hilbert?

1] Từ Định Lý Noether tới “Phương Trình của Chúa”:

Nói đến Emmy Noether lập tức phải nói đến Định Lý Noether, và phải biết rằng chính nhờ định lý này mà có Phương Trình Trường – xương sống của Thuyết Tương Đối Tổng Quát. Phương trình trường cho phép “thâu tóm” quy luật vật lý của vũ trụ ở tầm vĩ mô, nên tiến sĩ khoa học Amir Aczel gọi nó là “Phương trình của Chúa” (God’s Equation).

Trong cuốn God’s Equation[1], Aczel viết: “Năm 1917, Hilbert viết rằng công trình của ông đã nhận được sự giúp đỡ đắc lực của Emmy Noether … Nhưng Einstein cũng được giúp đỡ bởi công trình của Noether, người mà ông đã ca ngợi sau cái chết của bà năm 1935 như sau: “Theo nhận định của những nhà toán học giỏi nhất đang còn sống, Fraulein Noether là thiên tài sáng tạo toán học đáng kể nhất, kể từ khi nền giáo dục cao cấp dành cho phụ nữ bắt đầu …”. Einstein có lý do đúng đắn để mô tả Emmy Noether bằng những từ ngữ sáng chói như thế, vì nhờ định lý của bà mà Einstein đã rút ra hai hệ quả quan trọng cho phương trình trường hấp dẫn của ông … Thật thú vị để thấy rằng Emmy Noether – trực tiếp trong trường hợp thứ nhất (với Hilbert) và gián tiếp trong trường hợp thứ hai (với Einstein) – cuối cùng đã giúp cả hai đối thủ cạnh tranh trong cuộc chạy đua tìm ra những phương trình của Thuyết Tương Đối Tổng Quát”.

Một bài báo trên mạng nhan đề “Emmy Noether, Creative Mathematical Genius” (Emmy Noether, Thiên Tài Sáng Tạo Toán Học)[2] viết:

Năm 1915, Emmy Noether gia nhập Viện Toán ở Göttingen và bắt đầu làm việc với Klein[3] và Hilbert về thuyết tương đối tổng quát của Einstein. Năm 1918 bà đã chứng minh hai định lý trở thành cơ sở cho cả thuyết tương đối tổng quát lẫn vậy lý hạt cơ bản. Một định lý vẫn được gọi là Định Lý Noether … Cả Hilbert lẫn Albert Einstein đều phải nhờ cậy đến bà.

Năm 1915, Klein và Hilbert mời Noether cộng tác với họ tại Viện Toán Học ở Göttingen. Họ đang nghiên cứu những vấn đề toán học của thuyết tương đối tổng quát mới được báo cáo[5], và họ tin tưởng sự tinh thông của Noether sẽ giúp đỡ họ. Sau này Albert Einstein đã viết một bài báo cho cuốn Bách Khoa Toàn Thư Grolier 1955, trong đó ông nhấn mạnh ý nghĩa đặc trưng của thuyết tương đối bởi câu hỏi căn bản: “Các định luật tự nhiên phải được xây dựng sao cho chúng có giá trị như nhau đối với các hệ toạ độ bất kỳ (tiên đề về sự bất biến của các định luật tự nhiên đối với một phép biến đổi tuỳ ý của không gian và thời gian)?”. Một cách chính xác, đây chính là dạng bất biến trong các phép biến đổi mà Noether đã tập trung nghiên cứu trong toán học. Năm 1918, Noether đã chứng minh hai định lý tạo nên nền tảng cơ sở đối với thuyết thương đối tổng quát. Những định lý này đã xác nhận tính hợp lý của những mối quan hệ xác định mà các nhà vật lý thời đó đã nghi ngờ. Ngày nay một định lý được gọi là Định Lý Noether, định lý này thiết lập tính tương đương giữa một thuộc tính bất biến với một luật bảo toàn. Còn định lý kia liên quan đến mối quan hệ giữa một bất biến với sự tồn tại của những tích phân xác định của các phương trình chuyển động. Tháng 7 năm 1935, trên tạp chí Scripta Mathematica, nhà toán học lỗi lạc người Đức Hermann Weyl đã mô tả đóng góp của bà như sau: "Vào thời đó, bà đã cung cấp cho cả hai khía cạnh có ý nghĩa nhất của thuyết tương đối tổng quát một sự trình bầy toán học khái quát và chân xác nhất”.

Nếu Thuyết Tương Đối Tổng Quát là của Einstein và chỉ của Einstein mà thôi, thì những bằng chứng lịch sử cũng chỉ ra rằng người cung cấp cho Einstein những công cụ toán học cần thiết để hoàn thiện lý thuyết của mình chính là Emmy Noether! Giáo sư J. J. O'Connor và giáo sư E. F. Robertson ở Khoa Toán và Thống Kê thuộc Đại Học Saint Andrews ở Scotland nói:

Công trình đầu tiên của Emmy Noether khi bà vừa mới đặt chân tới Göttingen năm 1915 là một kết quả của vật lý lý thuyết mà đôi khi được gọi là Định Lý Noether. Định lý này chứng minh một quan hệ giữa tính đối xứng trong vật lý với các nguyên lý bảo toàn. Kết quả căn bản này trong thuyết tương đối tổng quát đã được Einstein ca ngợi trong một bức thư gửi cho Hilbert, trong đó ca ngợi Noether là người có tư tưởng toán học sâu sắc, thấu suốt (penetrating mathematical thinking). Chính công trình của bà về lý thuyết các bất biến đã dẫn tới việc toán học hoá một số khái niệm của thuyết tương đối tổng quát của Einstein. Ở đó, bà đã theo đuổi công trình toán học quan trọng xác nhận những phần chủ yếu của thuyết tương đối tổng quát.

Tưởng cũng nên nhắc lại rằng Thuyết Tương Đối Tổng Quát là “đỉnh Chomolungma trong dãy Hymalaya” của vật lý thế kỷ 20. Cái đỉnh này cao đến nỗi Einstein đã có lúc phải thốt lên lời “ngạc nhiên”: “Khi tôi nghĩ ra Thuyết Tương Đối Hẹp (Special Theory of Relativity), tôi cho rằng nếu tôi không nghĩ ra thì một ngày nào đó một người khác sẽ nghĩ ra, như Lorentz hay Poincaré chẳng hạn; Nhưng khi tôi nghĩ ra Thuyết Tương Đối Tổng Quát, tôi có cảm tưởng nếu tôi không nghĩ ra thì không biết đến bao giờ loài người mới nghĩ ra”. Nối tiếp nỗi ưu tư triết lý này, ta không khỏi đặt một câu hỏi tự nhiên: “Nếu không có Định Lý Noether thì không biết đến bao giờ loài người mới có Phương Trình Trường? Và nếu không có Phương Trình Trường thì bao giờ mới có Thuyết Tương Đối Tổng Quát?”.

2] Định lý về Đối Xứng và Cái Đẹp:

Định Lý Noether không chỉ giúp Einstein sáng tạo nên Phương Trình Trường, mà còn trở thành nền tảng của vật lý hiện đại – một lâu đài khoa học vật chất được xây dựng trên nền tảng đối xứng (symmetries) của các hạt cơ bản và của toàn bộ vũ trụ.

Người ta thường nói khoa học thế kỷ 20 có ba thành tựu vĩ đại nhất: Một là Thuyết Tương Đối của Einstein; Hai là Cơ Học Lượng tử của Heisenberg; Ba là Định Lý Bất Toàn của Kurt Godel. Nhưng sẽ là bất công nếu không nhắc đến thành tựu vĩ đại thứ tư – tư tưởng về tính đối xứng mà những công trình toán-lý của Noether đã tạo ra nền tảng: Toán học của Noether đã giúp các nhà vật lý của thế kỷ 20 xây dựng được lý thuyết các hạt cơ bản thành một thệ thống chặt chẽ, trong đó tính đối xứng vật lý và đối xứng toán học đóng vai trò nóng cốt.

Nhưng tư tưởng về tính đối xứng không dừng lại ở đó. Nó đang tiếp tục đóng vai trò chủ đạo trong những nghiên cứu mũi nhọn nhất của vật lý hiện đại.

Trong lúc nhận thấy tính đối xứng chi phối mọi cấu trúc vật chất trong vũ trụ, từ vũ trụ vi mô tới vĩ mô, các nhà khoa học cũng đồng thời nhận ra rằng tính đối xứng chính là tính cốt lõi của Cái Đẹp: Đối xứng là đặc trưng quan trọng nhất của Cái Đẹp, thậm chí có thể nói Đối Xứng chính là Cái Đẹp, hoặc Cái Đẹp phải đối xứng, …

Thực ra đó là điều nhân loại đã cảm nhận được từ rất lâu. Bài báo “Beauty” (Cái Đẹp), trên trang mạng Peaceful Mind[6] viết:

“Cái đẹp nằm trong mắt của kẻ ngắm nhìn” (Beauty is in the eyes of the beholder). Điều này đúng. Cái có thể đẹp với người này nhưng lại không đẹp với người khác. Do đó, ý kiến chủ quan (của mỗi người) dường như chỉ đúng với một hiện thực nhất định. (Trong khi đó), cái đẹp và cái gì là đẹp vẫn là trung tâm của nhiều cuộc thảo luận xuyên suốt lịch sử. Khi xem xét cái đẹp như một thứ ưu tiên trong đời sống thì nó trở thành vấn đề chăm sóc bản thân, gìn giữ bản thân, trân trọng bản thân, yêu bản thân. Cần hiểu rằng tất cả chúng ta đều đẹp! (Vì tuy rằng) Cái Đẹp bao gồm rất nhiều đặc trưng, có rất nhiều yếu tố tạo nên cái đẹp, nhưng đặc trưng đối xứng là rõ ràng nhất. Đối xứng có nghĩa là hai bên giống nhau, cân đối với nhau, cân xứng với nhau hoặc cân bằng nhau. Một khuôn mặt càng cân đối càng trở nên hấp dẫn. Nhìn vào thân thể con người cũng vậy, một cơ thể càng cân đối càng làm cho chúng ta cảm thấy người đó khoẻ mạnh. Qua quá trình lịch sử, sự cân đối này đã được coi như một dấu hiệu của những gien (gene) tốt, sức khoẻ tốt, sự sinh sản tốt và của cái đẹp.

Rất nhiều nghiên cứu về tính đối xứng của con người đã được thực hiện và nhiều người đã xác định công thức toán học cho cái đẹp. Điển hình nhất là bức tranh “Vitruvian Man” (Người đàn ông theo lý tưởng của Vitruvus) của Leonardo Da Vinci. Bức tranh này được Da Vincy vẽ như một nghiên cứu về những tỷ lệ của cơ thể đàn ông lý tưởng, được mô tả bởi nhà kiến trúc La Mã Vitruvus.

Cái Đẹp cũng đã được mô tả một cách toán học bởi khái niệm “Tỷ Lệ Vàng” (Golden Ratio). Công thức toán học dành cho cái đẹp này do Fibonacci đưa ra năm 1495, ông mô tả “những tỷ lệ vàng” như 1.618:1. “Tỷ lệ vàng” có thể được sử dụng để minh hoạ cho những tỷ lệ lý tưởng của cơ thể con người. Người ta cũng khám phá ra rằng tỷ lệ đó có mặt trong khắp tự nhiên và Vũ Trụ khi xem xét tính đối xứng của tất cả các vật.

Tuy nhiên, chỉ đến khi khoa học cho phép con người nhìn sâu vào thế giới hạ nguyên tử (thế giới vi mô) và nhìn rộng ra bên ngoài vũ trụ tới những khoảng cách xa hàng tỷ năm ánh sáng (thế giới vĩ mô) thì nhân loại mới thật sự nhận thấy tính đối xứng trong cấu trúc của Vũ Trụ là một bản chất phổ quát của Tự Nhiên. Bản chất ấy đã được Leon Lederman và Christopher Hill trình bầy một cách tuyệt vời trong cuốn “Symmetry and the Beautiful Universe” (Tính Đối Xứng và Vũ Trụ Đẹp Đẽ), với xuất phát điểm là Định Lý Noether.

Ngay từ Lời Nói Đầu, cuốn sách đã chỉ ra rằng Cái Đẹp hiện diện ở khắp mọi nơi và trên khắp mọi khía cạnh của cuộc sống:

Khi các nhà khoa học dùng kính viễn vọng để nhìn những vì sao xa xôi ngoài vũ trụ hoặc sử dụng những máy gia tốc hạt cơ bản khổng lồ để phân tích những thành phần nhỏ nhất của vật chất, họ khám phá ra những quy luật vật lý giống nhau cùng chi phối toàn thể vũ trụ ở mọi nơi mọi lúc. Các nhà vật lý nhận thấy một đặc trưng bất biến vĩnh cửu và phổ quát của các định luật vật lý là tính đối xứng. Hiện nay, tính đối xứng được xem là nguyên lý nền tảng xác định các định luật của tự nhiên, và kiểm soát toàn thể vũ trụ. Cái nhìn thấu suốt tối quan trọng này vào bên trong vật chất là một trong những đột phá nhận thức trong vật lý hiện đại và là cơ sở của những cố gắng đương đại nhằm khám phá ra một lý thuyết thống nhất lớn, như lý thuyết dây, để giải thích toàn bộ các định luật vật lý. Nhà vật lý từng đoạt Giải Nobel Leon Lederman và nhà vật lý lý thuyết Christopher Hill đã giải thích khái niệm tao nhã tột bậc về đối xứng và mọi biểu hiện sâu sắc của nó trong nghệ thuật, âm nhạc, và sự sống trên Trái Đất, từ những phần tử nhỏ nhất của vật chất, các quarks và leptons, đến Vũ Trụ ở phạm vi vĩ mô. Cuốn sách phổ biến khoa học hùng biện và không quá khó để đọc này không chỉ mô tả rõ ràng những khái niệm thường chỉ dành riêng cho các nhà vật lý và toán học, mà còn truyền cảm hứng thưởng thức cái đẹp sâu sắc vốn có của vũ trụ. Trung tâm của câu chuyện đẹp đẽ về tính đối xứng của vũ trụ lại không nằm trong cấu trúc của các hạt cơ bản hoặc các cụm thiên hà, mà nằm trong số phận của Emmy Noether, một nhà toán học nữ người Đức gốc Do Thái có tài năng thiên bẩm chói sáng, nhưng lúc sinh thời phải sống trong bóng tối (obscure) khổ hạnh (ascetic) và khiêm nhường (unpretentious). Mặc dù vẫn được ít người biết đến, nhưng bà đã để lại một ấn tượng về một nhà khoa học chẳng thua kém gì Albert Einstein, người đã ca tụng bà là có “tư duy toán học sắc sảo”. Trong một trong các công trình công bố sớm nhất, bà đã chứng mình rằng định luật bảo toàn năng lượng có liên hệ chặt chẽ với tính đối xứng và thời gian, và do đó việc thiết lập nền tảng toán học cho mối liên hệ đó có thể là cuộc cách mạng nhận thức quan trọng nhất của vật lý hiện đại. Lederman và Hill đã làm sáng tỏ những khái niệm về vũ trụ dựa trên công trình của Noether mà bấy lâu nay không được biết rộng rãi trong công chúng, đồng thời nêu lên những mối quan hệ dính líu giữa công trình của Noether với lý thuyết Big Bang, với thuyết tương đối tổng quát của Einstein, cơ học lượng tử và nhiều lĩnh vực khác của vật lý. Thông qua những mối quan hệ tương đồng tinh tế và những minh hoạ, Lederman và Hill đã mang những khái niệm đáng kinh ngạc này đến với đời sống. Cuốn sách này sẽ mở ra trước mắt bạn một thế giới mà bạn chưa từng thấy.

Xin lưu ý rằng Leon Lederman là người sáng lập ra Viện hàn lâm toán học và khoa học Illinois của Mỹ và từng đoạt Giải Nobel vật lý năm 1988, còn Christopher Hill là viện trưởng Viện vật lý lý thuyết thuộc Trung tâm máy gia tốc quốc gia Fermi của Mỹ. Họ nhìn Cái Đẹp trước hết bằng con mắt của vật lý, và Cái Đẹp đó trước hết biểu hiện dưới dạng đối xứng.

Và không chỉ Lederman và Hill coi nguyên lý đối xứng là nguyên lý phổ quát của vũ trụ, hầu như tất cả mọi nhà vật lý hiện nay đều có chung một cái nhìn như vậy. Những công trình nghiên cứu phức tạp nhất, khó khăn nhất của vật lý hiện nay chính là những công trình nghiên cứu về những cấu trúc siêu vi và siêu đối xứng, nhằm tìm ra một lý thuyết thống nhất cho toàn bộ vật lý – Lý thuyết hợp nhất Thuyết Tương Đối Tổng Quát với Cơ Học Lương Tử.

Thuyết Tương Đối được áp dụng cho vũ trụ vĩ mô và mang đặc trưng xác định, trong khi Cơ Học Lượng Tử được áp dụng cho thế giới vi mô và mang đặc trực bất định. Hai đặc trưng này hoàn toàn trái ngược nhau, do đó khát vọng của vật lý là tìm ra một lý thuyết thống nhất, có thể áp dụng cho toàn thể vũ trụ ở mọi cấp độ của không gian, từ vi mô đến vĩ mô.

Liệu có thể thống nhất hai đặc trưng trái ngược như thế với nhau không?

Đối với Einstein, khái niệm bất định chỉ để lộ ra sự bất lực về nhận thức của con người. Cho đến lúc rời khỏi thế giới, ông vẫn không thừa nhận nguyên lý bất định của Cơ Học Lượng Tử.

Nhưng Niels Bohr, nhà vật lý trứ danh người Đan Mạch, lại tin chắc vào nguyên lý bất định, và ông đã tìm cách “giải hoà” bằng một triết lý nổi tiếng được mệnh danh là “Nguyên Lý Bổ Sung”:

“Trái ngược không phải là mâu thuẫn, mà chúng bổ sung cho nhau”.

Tuy nhiên, chính Einstein lại là người khởi xướng việc xây dựng Lý Thuyết Trường Thống Nhất (Theory of Unified Field), với mong muốn hợp nhất trường hấp dẫn với trường điện từ. Mặc dù ông thất bại, nhưng tư tưởng của ông đã được hậu thế tiếp tục dưới tên gọi Lý Thuyết về Mọi Thứ (Theory of Everything), với tham vọng hợp nhất tất cả các trường lực đã biết trong Tự Nhiên. Tên gọi của lý thuyết này hàm ý nếu hợp nhất được tất cả các lực thì sẽ giải thích được mọi hiện tượng tự nhiên.

Lý thuyết này đã trở thành trung tâm của vật lý hiện đại, nơi thử thách những tài năng bậc nhất về vật lý và toán học.

Để giải quyết mâu thuẫn giữa xác định và bất định, giữa vĩ mô và vi mô, các nhà vật lý lý thuyết hướng tâm vào việc xây dựng mô hình của những thực thể nhỏ nhất của vũ trụ, cho phép giải thích được mọi tính chất vật lý trong mọi cấp độ vũ trụ. Việc tìm kiếm mô hình này trước hết là nhiệm vụ của các nhà vật lý lý thuyết. Bằng toán học và computer, họ xây dựng những mô hình đó, giống như cách đây nửa thế kỷ, các nhà sinh học cũng lao vào việc tìm kiếm cấu trúc của phân tử DNA nhằm giải thích mọi cơ chế di truyền của sự sống.

Một hướng phát triển được coi là khả quan nhất của Lý Thuyết về Mọi Thứ là Lý Thuyết Siêu Dây (Superstring Theory), trong đó các nhà vật lý đưa ra những mô hình của những thực thể đa chiều nhỏ bé nhất cấu tạo nên vũ trụ. Tất cả các mô hình này đều mang đặc trưng đối xứng. Mô hình hiện đại nhất là thực thể E8, được Kenneth Chang mô tả trên tờ The New York Times ngày 20-03-2007 như sau:

Đó là một trong những cấu trúc toán học đối xứng nhất trong vũ trụ. Cấu trúc đó có thể làm nền tảng cho Lý Thuyết về Mọi Thứ (Theory of Everything) mà các nhà vật lý đang tìm kiếm nhằm mô tả vũ trụ. Mười tám nhà toán học đã dành 4 năm trời cộng thêm 77 giờ đồng hồ để tính toán trên một siêu computer nhằm mục đích mô tả cấu trúc này, và kết quả đã được công bố vào ngày Thứ Hai tại một cuộc nói chuyện tại Viện Công Nghệ Massachusetts (MIT). Nhưng không dễ dàng mô tả thực thể này, ít nhất bằng ngôn ngữ (thông thường). Jeffrey D. Adams, giáo sự toán học của Đại Học Maryland và là người lãnh đạo dự án nghiên cứu E8, nói: “Đó là một thực thể trừu tượng tuyệt đẹp” . Đối với các nhà toán học và vật lý, đặc trưng đối xứng có thể có giúp họ nhìn thấu vào bên trong của thực thể ... “Thực ra bạn không thể vẽ được nó”, Brian Conrey, viện phó Viện Toán Học Mỹ, nói về E8, “Nó có một kiểu cong, một dạng torus[7] nào đó. Bây giờ bạn bắt đầu cho nó chuyển động quay tròn theo những cách khác nhau. Đó là một nhóm đối xứng thật kinh ngạc” ... Isaac Newton phát minh ra phép tính vi tích phân để nghiên cứu chuyển động của các vật thể. Giải tích Fourier, môn toán học về các mô hình tuần hoàn, được áp dụng hiệu quả trong việc nghiên cứu những hiện tượng như sóng ánh sáng, và các nhà vật lý sử dụng các nhóm Lie trong nghiên cứu cơ học lượng tử và lý thuyết tương đối. “Toàn bộ vật lý thế kỷ 20 đều gắn chặt với ngôn ngữ này”, tiến sĩ Conrey nói. E8 là một nhóm Lie làm nền tảng cho một số lý thuyết dây mà các nhà vật lý đang theo đuổi trong nỗ lực hợp nhất lực hấp dẫn với các lực cơ bản khác trong vũ trụ trong một lý thuyết duy nhất. “Rất có thể E8 sẽ xác định câu trúc sâu thẳm bên trong vũ trụ”, tiến sĩ Adams nói.

Không nghi ngờ gì nữa, đặc trưng đối xứng là một đặc trưng phổ quát của vũ trụ ở mọi cấp độ, từ siêu vi đến siêu vĩ. Đặc trưng ấy định hình Cái Đẹp của Tạo Hoá, trong đó có cái đẹp của con người.

Sản phẩm sáng tạo của con người, xét cho cùng cũng chỉ là sự phản ánh nhận thức của con người về Cái Đẹp, vì thế Cái Đẹp trong sáng tạo của con người cũng không thoát khỏi đặc trưng đối xứng.

Tóm lại, dù là một tác phẩm vật chất của tự nhiên hay một tác phẩm sáng tạo của con người, đều phản ánh cấu trúc đối xứng, đó là cấu trúc của Cái Đẹp, và cấu trúc ấy được giải thích một cách toán học bởi Định Lý Noether. Đó là lý do vì sao nhà khoa học John A. Gowan đã gọi Định Lý Noether là “Định lý về Chân Lý và Cái Đẹp”.

1-Lá cây; 2-Phân tử Carbon Tetrachloride; 3-Sao biển; 4-Xương rồng

Nhưng chua chát thay, trong khi Định Lý Noether bao trùm vũ trụ bao nhiêu thì số phận Emmy Nother lại cay đắng thiệt thòi bấy nhiêu.

3] Emmy Noether, cuộc đời và sự nghiệp:

Amalie Emmy Noether sinh ngày 23-03-1882 tại thị trấn Bavarian thuộc Erlangen, Đức, trong một gia đình trung lưu Đức gốc Do Thái. Bố của Emmy, Max Noether, cũng từng là một nhà toán học xuất sắc, giáo sư tại Đại Học Erlangen.

Xuất thân trong một gia đình Do Thái buôn bán ở Đức, Max Noether bị bệnh bại liệt năm 14 tuổi; Sau khi hồi phục được cử động, ông vẫn bị tật nguyền một chân. Hầu hết là tự học, ông đã nhận được bằng tiến sĩ của Đại Học Heidelberg năm 1868. Sau khi dạy học ở đó 7 năm, ông kiếm được công việc tại Bavarian thuộc Erlangen, tại đây ông gặp và cưới Ida Amalia Kaufmann, con gái một thương gia Do Thái giầu có. Với tư cách một nhà toán học, Max Noether đóng góp chủ yếu cho hình học đại số, đi theo con đường của Alfred Clebsch. Thành tựu nổi tiếng nhất của ông là định lý Brill–Noether và định lý AF+BG; Tuy nhiên ông cũng nổi tiếng vì một số định lý khác.

Emmy Noether là con đầu trong 4 người con trong gia đình. Tên đầu tiên của bà là Amalie, đặt theo tên mẹ và bà nội, nhưng bà đã sử dụng tên giữa ngay từ khi còn trẻ.

Lúc nhỏ, thông minh và tính tình cởi mở, Emmy bị cận thị và nói ngọng. Nhiều năm về sau, một người bạn của gia đình kể lại một câu chuyện về Emmy lúc nhỏ, rằng cô bé này giải rất nhanh những trò đố vui thách thức trí não trong một cuộc hội hè của trẻ con, thể hiện một sự nhậy bén về lôgích như một cô gái lớn tuổi. Emmy cũng được dạy học nấu ăn và nội trợ – như hầu hết các cô gái thời đó – và học piano. Nhưng Emmy không thích thú những môn học đó, mặc dù cô thích khiêu vũ. Trong 3 em trai, chỉ có Fritz Noether, sinh năm 1884 là có những thành tựu về nghiên cứu khoa học. Sau khi học ở Munich, Fritz nổi tiếng trong lĩnh vực toán ứng dụng. Cậu em lớn nhất, Alfred, sinh năm 1883, đậu tiến sĩ hoá học tại ĐH Erlangen năm 1909, và mất chín năm sau. Cậu em út, Gustav Robert, sinh năm 1889, ốm đau kinh niên và mất năm 1928.

Nhưng giống như Marie Curie, Emmy Noether đã mất những năm quý báu thời trẻ chỉ vì là phụ nữ. Không ai trong gia đình Noether nghĩ rằng Noether có thể làm được gì nhiều hơn là hoàn thành một nền giáo dục dành cho con gái những gia đình trung lưu vào thời bấy giờ. Muốn học tiếp, Noether phải tự thân vận động. Cô mất ba năm để theo một chương trình sư phạm, một trong một vài cơ hội hiếm hoi dành cho phụ nữ lúc đó. Hoàn thành chương trình này, Noether nhắm tới Đại Học Erlangen, nơi cha cô là giáo sư. Nhưng đại học ở Đức lúc đó không nhận sinh viên nữ. Nhờ sự thông cảm của một số giáo sư tốt bụng, Noether chỉ được ngồi trong lớp với tư cách dự thính viên, thay vì trở thành sinh viên chính thức. Dẫu sao thì đó vẫn là một may mắn, vì đa số giáo sư Đức thời đó vẫn cho rằng chương trình đại học vượt quá khả năng tư duy của phụ nữ.

Trong cuốn Pythagoras’ Trousers (Dịch ý: Những môn đệ của Pythagore), Margaret Wertheim viết: “Giống như trong thời trung cổ, một nhà hàn lâm đã tuyên bố rằng việc để cho phụ nữ xâm lăng vào các trường đại học là … một biểu hiện đáng xấu hổ của sự yếu kém về đạo đức” (!).

Tuy nhiên sau 5 năm dự thính, niềm say mê khao khát học hỏi của Noether đã làm các giáo sư cảm động, và cô được nhận làm sinh viên chính thức. Chẳng bao lâu sau Noether đã hoàn thành luận án tiến sĩ khoa học tại Đại Học Erlangen một cách xuất sắc kèm theo phần thưởng danh dự. Nhưng giành được mảnh bằng không có nghĩa là sẽ kiếm được một việc làm chính thức: 8 năm tiếp theo kể từ khi có bằng tiến sĩ, Noether phải làm việc không lương cho trường đại học mà cha của bà đang là giáo sư. Bà đã hướng dẫn luận án tiến sĩ cho nhiều sinh viên, giảng bài cho họ, tiếp tục theo đuổi những nghiên cứu của riêng mình. Khi bệnh tình của cha nặng lên, bà đã đảm nhiệm luôn nhiệm vụ của ông tại trường đại học nhưng vẫn không được công nhận chính thức. Bà không được đa số đồng nghiệp ủng hộ. Vì sao vậy?

Theo nhà viết tiểu sử Sharon McGrayne, Noether là một người phụ nữ đáng yêu, cởi mở, không hề kiêu căng tự phụ, tính tình thoải mái, không bận tâm đến những quy ước nữ tính đương thời, ăn mặc giản dị, không màng đến thời trang, người to béo quá khổ, tính tình nồng nhiệt, hăng hái phát biểu ý kiến, khá bừa bộn, lúc nào cũng bù đầu vì công việc.

McGrayne nhận xét rằng Einstein cũng có những tính cách tương tự, nhưng trong khi tính giản dị luộm thuộm của Einstein được người đời tán tụng là biểu hiện “đãng trí bác học” thì Noether lại bị người đời chế giễu là thiếu nữ tính và bị xa lánh. Đa số các giáo sư không thích chia sẻ với một người phụ nữ mà họ cho là thiếu nữ tính.

Năm 1914, David Hilbert cùng cộng sự của ông là Felix Klein đã “để mắt” tới những nghiên cứu của Noether. Họ mời Noether về Đại Học Gottingen, đại học số 1 Châu Âu thời đó, để cộng tác nghiên cứu. Trong suốt 5 năm trời tại Gottingen, Noether đã sản xuất ra những công trình vĩ đại nhất trong sự nghiệp sáng tạo của bà, trong đó có việc giúp đỡ cả Hilbert lẫn Einstein trong việc hoàn thiện Phương Trình Trường. Nhưng đến lúc đó bà vẫn phải làm việc không công, không được trả lương! Đơn giản vì bà vẫn không được công nhận làm giáo sư chính thức. Thực tế bà đã đứng trên bục giảng của trường đại học danh tiếng bậc nhất thế giới này để giảng bài như một giáo sư, nhưng lại phải đội tên Hilbert: Giáo sư Hilbert phải đứng tên trên các thông báo chính thức về lớp học do bà đứng giảng. Suốt thời gian đó, bà chỉ có một thu nhập nhỏ nhoi từ một quỹ đóng góp của các nhà hảo tâm do mẹ của bà đứng ra vận động mà thôi.

Cả Hilbert lẫn Klein đều thấy rõ sự bất công trong việc đối xử của trường đại học với Noether và cả hai đều ra sức vận động công nhận chức giáo sư chính thức cho bà. Nhưng ngay cả những tiếng nói có uy tín nhất như thế cũng không làm thay đổi nổi tình hình. Sự chống đối Noether vẫn tiếp tục. Thậm chí trong những cuộc tranh luận về việc công nhận Noether, vẫn có những ý kiến cho rằng chức năng của phụ nữ là ở nhà trông nom nuôi dạy con cái chứ không phải đứng trên bục giảng đại học!

Nhưng trước sự hối thúc của Hilbert, cuối cùng thì khoa toán đã thông báo ý định bổ nhiệm Noether vào một chức phó giáo sư (junior position). Nhưng lập tức ý định này bị các giáo sư ở khoa khác phản đối. Một vị lên tiếng: “Được vào Hội đồng giáo sư thì rồi bà ấy sẽ trở thành một giáo sư và trở thành một thành viên của ban giám hiệu nhà trường. Nên chăng để cho một phụ nữ trở thành thành viên ban giám hiệu một trường đại học?”. Hilbert trả lời: “Thưa quý vị, tôi không nghĩ rằng vấn đề giới tính lại trở thành một lý do để chống lại việc tiếp nhận bà ấy. Và sau hết, ban giám hiệu không phải là một nhà tắm (ý nói chỉ ở nhà tắm mới cần phân biệt giới tính)”.

Bất chấp lời biện hộ của Hilbert, Bộ Giáo Dục Đức đồng ý với ý kiến chống đối Noether. Phải đợi mãi đến năm 1921, sau khi nước Đức thua trận trong cuộc Đại Chiến Thế Giới I, tình hình xã hội và chính trị ở Đức có những thay đổi căn bản, ý thức xã hội có phần cởi mở hơn thì lúc đó Noether mới được công nhận chức phó giáo sư, nhưng vẫn là một phó giáo sư làm việc không công, không được trả lương (!!!). Điều này quả là quá khó hiểu đối với chúng ta ngày nay.

Tóm lại, trong suốt 18 năm làm việc tại Đại Học Gottingen, Noether chưa bao giờ được công nhận giáo sư chính thức và được hưởng một đồng lương chính thức. Bà cũng chưa bao giờ nhận được sự tài trợ từ bất kỳ một cơ quan nào thuộc hệ thống nhà nước hoặc xã hội, không được hưởng tiền hưu trí hay một khoản bảo trợ xã hội nào khác.

Và bất chấp những đóng góp khoa học mà một người như Hilbert cũng phải chịu ơn và kính phục, Viện hàn lâm khoa học hoàng gia Gottingen đã từ chối bầu Noether làm viện sĩ. Tệ hơn nữa, tên tuổi Emmy Noether cũng không bao giờ được đưa vào danh sách những nhà toán học hàng đầu trên các tạp chí toán học quốc tế mà chính bà đã từng giúp đỡ việc biên tập!

Năm 1933, Hitler lên nắm chính quyền ở Đức, chủ nghĩa quốc xã phát động một cao trào bài Do Thái chưa từng có. Tất cả các nhà bác học Đức gốc Do Thái như Albert Einstein, Herman Weyl, Lise Meitner, Emmy Noether, … đều phải tìm đường trốn ra ngoại quốc. Nhưng trong khi những người như Einstein, Weyl lập tức được người Mỹ trọng vọng, phong chức giáo sư tại Viện nghiên cứu tiên tiến Princeton (Institute for Advanced Study, Princeton) thì Noether không được một trường đại học nào tiếp nhận. Cuối cùng bà chỉ tìm được một công việc bình thường tại một trường cao đẳng dành cho phụ nữ mang tên Bryn Mawr. Bà vẫn vui vẻ làm việc, vì thực ra bà chỉ cần có một chỗ làm để tiếp tục những nghiên cứu của mình mà thôi.

Năm 1935, đúng vào lúc Viện nghiên cứu tiên tiến Princeton có ý định mời Noether vào làm việc thì bà lâm bệnh và đột ngột ra đi – Bà mất sau một ca mổ cắt bỏ khối u nang buồng trứng. Trước khi mổ, bà vẫn đùa: “Tôi sẽ giảm cân!”, vì bà vốn có khổ người to béo. Tính hài hước của bà và “sự may mắn” do Viện Princeton mang đến đúng lúc bà ra đi đã làm dấy lên trong lòng nhiều người một cảm giác chua chát. “Lúc vui nhất là lúc nên về”, lời bất hủ này của William Sheakspere mấy trăm năm trước dường như ứng vào định mệnh của Emmy Noether!

Hơn bất kỳ một vở bi kịch nào khác, cuộc đời của Emmy Noether là một sự tương phản đầy nghịch lý giữa một tài năng siêu phàm với một cương vị thấp kém, giữa một cống hiến vĩ đại với một đền đáp bạc bẽo.

“Ca mổ của Emmy Noether làm cho thế giới không chỉ mất đi một nhà toán học vĩ đại, mà còn mất đi một người phụ nữ vĩ đại!”, đó là lời điếu của nhà bác học trứ danh Herman Weyl dành cho người phụ nữ tài hoa bạc mệnh này.

● Emmy Noether mất ngày 23-04-1935. Vài ngày sau, ngày 5-5-1935, tờ New York Times công bố điếu văn của Albert Einstein dành cho người phụ nữ thiên tài bậc nhất, trong đó viết:

Cố gắng của hầu hết mọi người đều bị tiêu hao trong cuộc đấu tranh giành giật cơm áo hàng ngày, … nhưng may mắn thay, có một số ít người sớm nhận thấy rằng những trải nghiệm đẹp nhất và thoả mãn nhất trong đời họ không đến từ thế giới bên ngoài, mà nẩy sinh từ nội tâm – từ sự phát triển của cảm xúc, tư duy và hành động của cá nhân mình. Những nghệ sĩ chân chính, những nhà nghiên cứu và những nhà tư tưởng luôn luôn nằm trong số đó. Bất luận số phận của họ ra sao, kết qủa của những nỗ lực của họ là phần đóng góp có giá trị nhất mà mỗi thế hệ có thể tạo ra cho thế hệ kế tiếp. Vài ngày trước đây, một nhà toán học xuất chúng, Giáo sư Emmy Noether, một người trước đây từng làm việc tại Đại Học Göttingen và hai năm qua tại trường Cao Đẳng Bryn Mawr, đã mất ở tuổi 53. Theo nhận định của những nhà toán học giỏi nhất đang còn sống, Fraulein Noether là thiên tài sáng tạo toán học đáng kể nhất, kể từ khi nền giáo dục cao cấp dành cho phụ nữ bắt đầu …

● Năm 1983, Grace Quinn viết trên một biểu trưng tôn vinh Emmy Noether: Emmy Noether được nhớ đến như một tư tưởng chói sáng, một tính cách đẹp đẽ, lòng can đảm bất khuất, thiên hướng dân chủ, một người tràn đầy tình yêu đối với cuộc sống và toán học.

Emmy Noether là một nhà toán học nữ người Đức gốc Do Thái, nổi tiếng vì những đóng góp có ảnh hưởng sâu xa trong đại số trừu tượng. Thường được mô tả như người phụ nữ quan trọng nhất trong lịch sử toán học, bà đã tạo nên cuộc cách mạng về lý thuyết vòng, trường và đại số. Bà cũng nổi tiếng vì những đóng góp trong vật lý hiện đại; hai định lý Noether đã giải thích mối liên hệ giữa tính đối xứng với các định luật bảo toàn, và là công cụ chủ yếu trong nghiên cứu của các nhà vật lý toán.

● Trong một bài báo nhan đề “Creative Mathematical Genius” (Thiên Tài Sáng Tạo Toán Học), Trung Tâm Siêu Computer San Diego (San Diego Super Computer Center) của Mỹ nhận định[1]: Emmy Noether là người được sinh ra để trở thành nhà toán học vĩ đại.

Sự hiểu biết về đối xứng như một nền tảng căn bản của các lý thuyết vật lý đã được trình bầy bởi chính Emmy Noether, một phụ nữ đã trở thành nhà toán học vào thời kỳ mà tại nước Đức quê hương của bà, phụ nữ không được tham gia vào công việc tại các trường đại học nếu không có sự cho phép đặc biệt, và không được đứng trên bục giảng dạy sinh viên … Chính sự tổng quát hoá các tính chất đối xứng đã tạo nên cơ sở của Mô Hình Tiêu Chuẩn (Standard Model) của vật lý các hạt cơ bản và của hầu hết các vật lý lý huyết hiện đại.

Mối liên hệ giữa tính đối xứng và các định luật bảo toàn là một trong những khám phá vĩ đại nhất của vật lý thế kỷ 20. Nhưng tôi nghĩ rất ít chuyên gia đã được biết điều đó hoặc biết người khám phá ra điều đó — Emily Noether, một nhà toán học Đức (gốc Do Thái). Đó là một tư tưởng cốt yếu của vật lý thế kỷ 20, ngang với tư tưởng cho rằng không thể vượt qua tốc độ ánh sáng …

● Thay cho lời kết là một nhận định của trang mạng[3] Answers.com :

Noether là một phần của khoa toán thuộc Đại Học Göttingen trong những năm 1920, khi mà danh tiếng của đại học này về nghiên cứu và giảng dạy toán học được coi là cao nhất thế giới. Mặc dù vậy, ngay cả với sự giúp đỡ của nhà toán học khả kính Hermann Weyl, Noether vẫn không sao có được một vị trí giảng dạy chính thức ở đó, tương đương với những đồng nghiệp nam của bà. Một lần chính Weyl phải thốt lên: “Tôi lấy làm xấu hổ vì đã chiếm một vị trí được ưu đãi hơn so với bà, người mà tôi biết là giỏi hơn tôi với tư cách một nhà toán học rất đáng kính”.

[1] Nguyên văn: “It might be that Emmy Noether was designed for mathematical greatness”. Xem trang web: http://www.astr.ua.edu/4000WS/NOETHER.html

[2] Xem “Emmy Noether, symmetry and conservation laws”

http://www.scientificblogging.com/lattice_points/emmy_noether_symmetry_and_conservation_laws

[3] http://www.answers.com/topic/emmy-noether-1

Emmy Noether

Emmy Noether (1882-1935), người phụ nữ đã giúp Einstein hoàn thiện Thuyết Tương Đối

1] Từ Định Lý Noether tới “Phương Trình của Chúa”:

2] Định lý về Đối Xứng và Cái Đẹp:

3] Emmy Noether, cuộc đời và sự nghiệp: